前言
训练网络的一种方法是，通过反复计算实际输出和期望输出之间的差异，然后改变网络的参数值来缩小该差异，从而使损失最小化，或其输出中的误差最小。梯度下降缩小了误差，使计算损失的函数最小化。使用梯度下降，你也有可能被困在一个由多个山谷（局部最小值）、山峰（局部最大值）、马鞍（马鞍点）和高原组成的非凸形景观中。事实上，像图像识别、文本生成和语音识别这样的任务都是非凸的，而且已经出现了许多梯度下降的变体来处理这种情况。
梯度下降法的实现方式
通俗易懂讲解梯度下降法！ 蛮不错的一篇文章。
关于神经网络，一个学术界搞错了很多年的问题BP算法自八十年代发明以来，一直是神经网络优化的最基本的方法。神经网络普遍都是很难优化的，尤其是当中间隐含层神经元的个数较多或者隐含层层数较多的时候。长期以来，人们普遍认为，这是因为较大的神经网络中包含很多局部极小值（local minima），使得算法容易陷入到其中某些点。到2014年，一篇论文《Identifying and attacking the saddle point problem in high-dimensional non-convex optimization》，指出高维优化问题中根本没有那么多局部极值。作者依据统计物理，随机矩阵理论和神经网络理论的分析，以及一些经验分析提出高维非凸优化问题之所以困难，是因为存在大量的鞍点（梯度为零并且Hessian矩阵特征值有正有负）而不是局部极值。
bias 偏差 和 variance 方差
一文读懂深度学习：从神经元到BERT 形象的说，拟和就是把平面上一系列的点，用一条光滑的曲线连接起来。因为这条曲线有无数种可能，从而有各种拟和方法。拟和的曲线一般可以用函数表示，根据这个函数的不同有不同的拟和的名字：欠拟合（underfitting） 和过拟合（overfitting）
假设存在多个数据集\(D_1,D_2,…\)，
f(x;D)由训练集 D 学得的模型 f 对 x 的预测输出。- y 表示x 的真实值
-
针对所有训练集，学习算法 f 对测试样本 x 的 期望预测 为:
\[\overline{f}(x)=E_D[f(x;D)]\] -
偏差，偏差度量了学习算法的期望预测与真实结果的偏离程度，即刻画了学习算法本身的拟合能力。
\[偏差=(\overline{f}(x)-y)^2\] -
方差，方差度量了同样大小的训练集的变动所导致的学习性能的变化，即刻画了数据扰动所造成的影响。
\[方差=E_D[(f(x;D)-\overline{f}(x))^2]\]
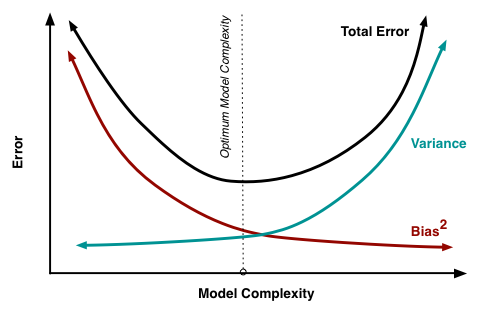
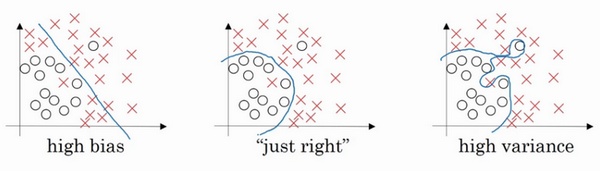
我们希望偏差与方差越小越好，但一般来说偏差与方差是有冲突的, 称为偏差-方差窘境 (bias-variance dilemma).
- 给定一个学习任务, 在训练初期, 由于训练不足, 学习器的拟合能力不够强, 偏差比较大, 也是由于拟合能力不强, 数据集的扰动也无法使学习器产生显著变化, 也就是欠拟合的情况;
- 随着训练程度的加深, 学习器的拟合能力逐渐增强, 训练数据的扰动也能够渐渐被学习器学到;
- 充分训练后, 学习器的拟合能力已非常强, 训练数据的轻微扰动都会导致学习器发生显著变化, 当训练数据自身的、非全局的特性被学习器学到了, 则将发生过拟合.
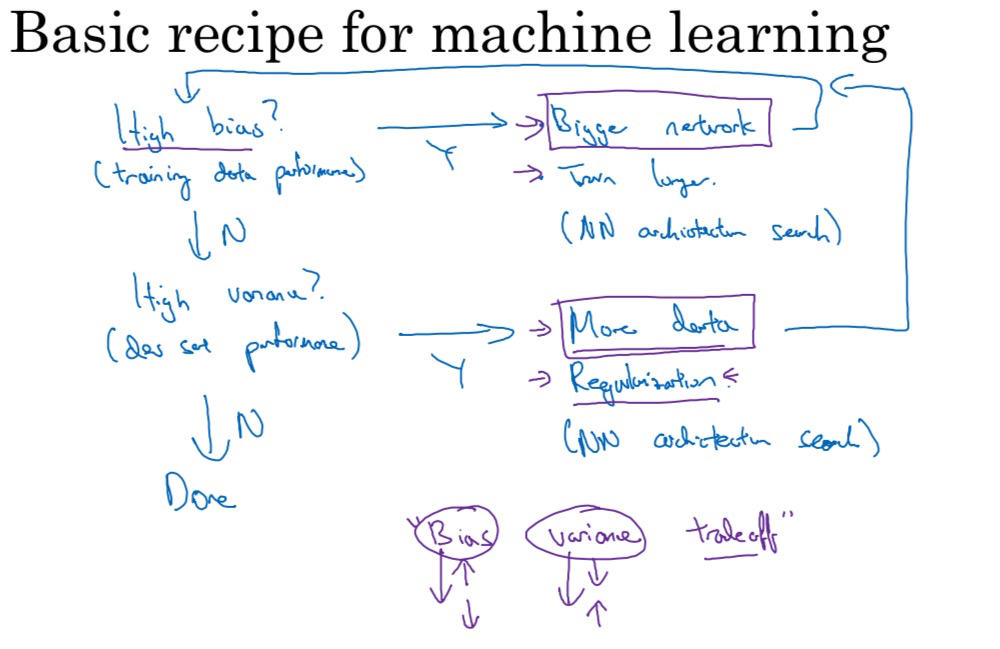
- 初始训练模型完成后，我们首先要知道算法的偏差高不高
-
如果偏差很高，甚至无法拟合训练集，可以尝试
- 更大的网络 比如更多的隐层或隐藏单元
- 花费更多的时间训练算法
- 更先进的优化算法
- 新的神经网络结构
- 准备更多的训练数据对高偏差没啥大用
- 反复尝试，直到可以拟合训练集，使得偏差降低到可以接受的值
-
如果方差比较高
- 更多的训练数据
- regularization/正则化
- 新的神经网络结构
- 不断尝试，直到找到一个低偏差、低方差的框架
防止过拟合
数学原理上理解起来还比较困难
如果测试集的评估结果相比训练集出现大幅下降，比如下降幅度超过了 5%，就说明模型产生了非常严重的过拟合现象，我们就要反思一下是不是在模型设计过程中出现了一些问题。当模型相对于训练数据的数量和噪度都过于复杂时（模型的层数或者每层的神经元数量过多），可能的解决方案如下
- 简化模型：可以选择较少参数的模型（例如，选择线性模型而不是高阶多项式模型）也可以减少训练数据中的属性数量，或者是约束模型。
- 收集更多的训练数据。
- 减少训练数据中的噪声（例如，修复数据错误和消除异常值）。
- 看一看是不是需要加入 Dropout、正则化项来减轻过拟合的风险。
欠拟合和过拟合正好相反。它的产生通常是因为对于底层的数据结构来说，你的模型太过简单。例如，用线性模型来描述生活满意度就属于欠拟合。现实情况远比模型复杂得多，所以即便是对于用来训练的示例，该模型产生的预测都一定是不准确的。解决这个问题的主要方式有：
- 选择一个带有更多参数、更强大的模型。
- 给学习算法提供更好的特征集（特征工程）。
- 减少模型中的约束（例如，减少正则化超参数）。
正则化/规则化——给损失函数“加码”
假设一个神经网络样本为
\[\begin{Bmatrix} (x^{(i)},y^{(i)}),i=1,...m \end{Bmatrix}\]训练过程中训练样本的预测结果为
\(\hat y^i,i =1,...m\) 损失函数
\[J(w,b)=\frac{1}{m}\sum\_{i=1}^mL(\hat y^i , y^i)\]L2正则化是给cost function加上正则项
\[J(w,b)=\frac{1}{m}\sum\_{i=1}^mL(\hat y^i , y^i)+\frac{\lambda}{2m}||w||_2^2\]梯度下降时 \(W=W-\sigma d_w\)
加入L2 正则项之后，相当于在原来 \(d_w\) 的基础上带上
\[\frac{d}{d_W}(\frac{\lambda}{2m}W^2)=\frac{\lambda}{m}W\]\(d_w\) 变得更大，W会变得更小
L1正则化采用的正则化项如下所示
\[J(w,b)=\frac{1}{m}\sum\_{i=1}^mL(\hat y^i , y^i)+\frac{\lambda}{2m}||w||_1\]为什么正则化有利于预防过拟合呢？为什么它可以减少方差问题？我们通过两个例子来直观体会一下
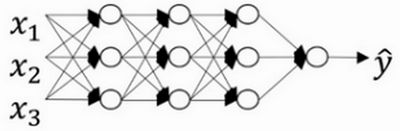
可以想象这是一个过拟合的神经网络。我们添加正则项，它可以避免数据权值矩阵过大，这就是弗罗贝尼乌斯范数，为什么压缩范数，或者弗罗贝尼乌斯范数或者参数可以减少过拟合？
直观上理解就是如果正则化设置得足够大，权重矩阵被设置为接近于0的值，直观理解就是把多隐藏单元的权重设为0，于是基本上消除了这些隐藏单元的许多影响。如果是这种情况，这个被大大简化了的神经网络会变成一个很小的网络，小到如同一个逻辑回归单元，可是深度却很大，它会使这个网络从过度拟合的状态更接近左图的高偏差状态。但是会存在一个中间值，于是会有一个接近“Just Right”的中间状态。
直观理解就是增加到足够大，会接近于0，实际上是不会发生这种情况的，我们尝试消除或至少减少许多隐藏单元的影响，最终这个网络会变得更简单，这个神经网络越来越接近逻辑回归，我们直觉上认为大量隐藏单元被完全消除了，其实不然，实际上是该神经网络的所有隐藏单元依然存在，但是它们的影响变得更小了。
我们进入到神经网络内部来直观感受下为什么正则化会预防过拟合的问题，假设我们采用了tanh的双曲线激活函数
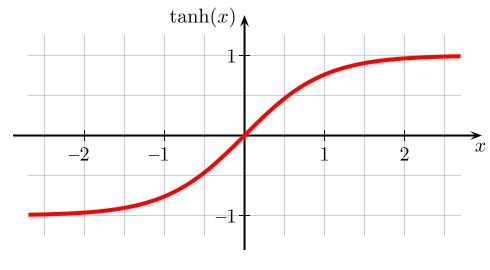
如果使用了正则化部分，那么权重W会倾向于更小，因此得到的 \(Z^{[l]}=W^{[l]}A^{[l-1]}+b^{[l]}\) 会更小，在作用在激活函数的时候会接近于上图中横轴零点左右的部分。如果 Z 的值最终在这个范围内，都是相对较小的值， \(g(z)=tanh(z)\) 大致呈线性（上图横轴零点左右的部分大致是直线），“边界”越线性，“弯曲度”就会小一点，网络从过拟合逐步向高偏差状态靠拢。
模型验证
模型训练的目标是找到拟合能力和泛化能力的平衡点，拟合能力代表模型在已知数据上表现得好坏，泛化能力代表模型在未知数据上表现得好坏。如果算法工程师想让拟合能力足够好，就需要构建一个复杂的模型对训练集进行训练，可越复杂的模型就会越依赖训练集的信息，就很可能让模型在训练集上的效果足够好，在测试集上表现比较差，产生过拟合的情况，最终导致模型泛化能力差。这个时候，如果算法工程师想要提高模型的泛化能力，就要降低模型复杂度，减少对现有样本的依赖，但如果过分地减少对训练样本的依赖，最终也可能导致模型出现欠拟合的情况。
模型验证主要是对待验证数据上的表现效果进行验证，验证数据与训练数据的格式完全一样，但内容没有重叠。这样才能验证模型能否在该任务上进行泛化，而不仅仅是记住了训练数据。一般是通过模型的性能指标和稳定性指标来评估。
- 首先是模型性能。模型性能可以理解为模型预测的效果，你可以简单理解为“预测结果准不准”，它的评估方式可以分为两大类：分类模型评估和回归模型评估
- 分类模型解决的是将一个人或者物体进行分类，例如在风控场景下，区分用户是不是“好人”，或者在图像识别场景下，识别某张图片是不是包含人脸。对于分类模型的性能评估，我们会用到包括召回率、F1、KS、AUC 这些评估指标。
- 回归模型解决的是预测连续值的问题，如预测房产或者股票的价格，所以我们会用到方差和 MSE 这些指标对回归模型评估。 我们除了要知道可以对模型性能进行评估的指标都有什么，还要知道这些指标值到底在什么范围是合理的。虽然，不同业务的合理值范围不一样，我们要根据自己的业务场景来确定指标预期，但我们至少要知道什么情况是不合理的。比如说，如果算法同学跟我说，AUC 是 0.5，我想都不想就知道，这个模型可能上不了线了，因为 AUC = 0.5 说明这个模型预测的结果没有分辨能力，准确率太差，这和瞎猜得到的结果几乎没啥区别，那这样的指标值就是不合理的。
- 模型的稳定性，你可以简单理解为模型性能（也就是模型的效果）可以持续多久。我们可以使用 PSI 指标来判断模型的稳定性，如果一个模型的 PSI > 0.2，那它的稳定性就太差了，这就说明算法同学的工作交付不达标。