简介
卷积神经网络数学原理解析 未读
卷积: 计算机的眼睛
卷积运算是深度学习和神经网络中常用的一种操作,用于从输入数据中提取特征。在深度学习中,卷积运算通常与激活函数(如 ReLU)、池化层等结合使用,构成卷积神经网络(CNN),用于提取并学习数据中的特征,从而实现图像识别、分类、分割等任务。
在使用卷积之前,人们尝试了很多人工神经网络来处理图像问题,但是人工神经网络的参数量非常大,从而导致非常难训练。举例说来,一个尺寸为200x200x3的图像,会让神经元包含200x200x3=120,000个权重值。而网络中肯定不止一个神经元,那么参数的量就会快速增加!显而易见,这种全连接方式效率低下,大量的参数也很快会导致网络过拟合。到卷积神经网络的出现,它的两个优秀特点:稀疏连接与平移不变性,就是稀疏连接可以让学习的参数变得很少,而平移不变性则不关心物体出现在图像中什么位置。
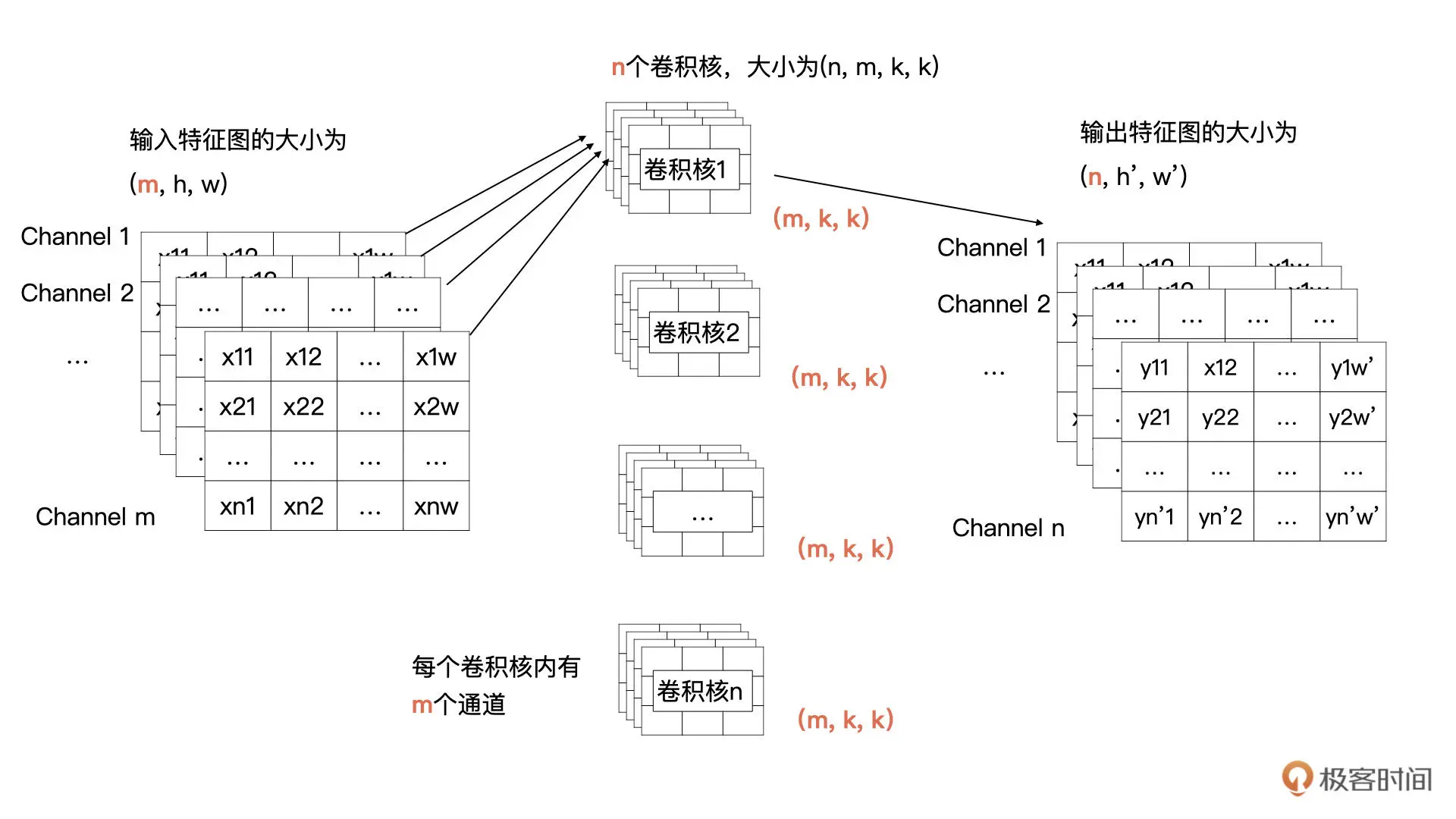
输入只有 1 个通道,现在有多个通道了(一个图片有RGB 和透明度4个通道),那我们该如何计算呢?其实计算方式类似,输入特征的每一个通道与卷积核(卷积核的大小为 k * k)中对应通道的数据按我们之前讲过的方式进行卷积计算(输入特征图有 m 个通道,所以每个卷积核里要也要有 m 个通道),也就是输入特征图中第 i 个特征图与卷积核中的第 i 个通道的数据进行卷积。这样计算后会生成 m 个特征图,然后将这 m 个特征图按对应位置求和即可,求和后 m 个特征图合并为输出特征中一个通道的特征图。
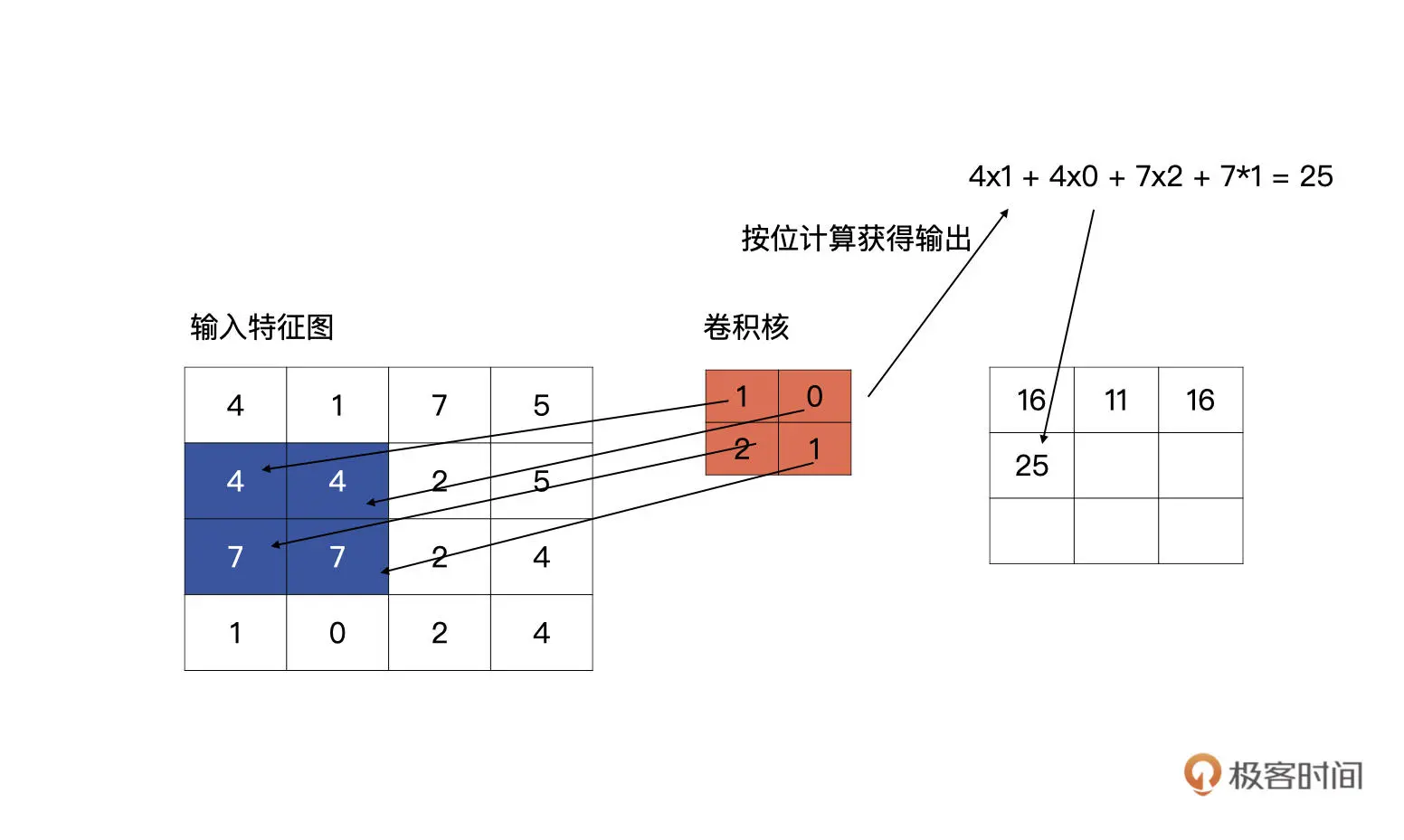
pytorch nn.Conv2d 对输入计算卷积 就是一行代码
import torch
import torch.nn as nn
input_feat = torch.tensor([[4, 1, 7, 5], [4, 4, 2, 5], [7, 7, 2, 4], [1, 0, 2, 4]], dtype=torch.float32)
print(input_feat)
# 一般不会干预卷积核的初始化,kernel_size 是卷积核的高宽,stride 为滑动的步长,padding 为补零的方式
conv2d = nn.Conv2d(1, 1, (2, 2), stride=1, padding='same', bias=False)
output = conv2d(input_feat)
CNN
卷积神经网络主要由三种类型的层构成:卷积层,汇聚(Pooling)层和全连接层(全连接层和常规神经网络中的一样)
卷积神经网络 CNN 是含有卷积层的神经网络。CNN 新增了卷积核大小、卷积核数量、填充、步幅、输出通道数等超参数。
- 卷积层保留输入形状,使图像的像素在高和宽两个方向上的相关性均可能被有效识别。
- 卷积层通过滑动窗口将同一卷积核与不同位置的输入重复计算,从而避免参数尺寸过大。
卷积层的参数是由一些可学习的滤波器集合构成的。每个滤波器在空间上(宽度和高度)都比较小,但是深度和输入数据一致。在每个卷积层上,我们会有一整个集合的滤波器(比如12个),每个都会生成一个不同的二维激活图。将这些激活映射在深度方向上层叠起来就生成了输出数据。
在处理图像这样的高维度输入时,让每个神经元都与前一层中的所有神经元进行全连接是不现实的。相反,我们让每个神经元只与输入数据的一个局部区域连接。该连接的空间大小叫做神经元的感受野(receptive field),它的尺寸是一个超参数(其实就是滤波器的空间尺寸)。在深度方向上,这个连接的大小总是和输入量的深度相等。需要再次强调的是,我们对待空间维度(宽和高)与深度维度是不同的:连接在空间(宽高)上是局部的,但是在深度上总是和输入数据的深度一致。
卷积层每个层的输入是3D数据,然后使用一个可导的函数将其变换为3D的输出数据。有的层有参数,有的没有(卷积层和全连接层有,ReLU层和汇聚层没有)。
LeNet
提起卷积神经网络,也许可以避开VGG、GoogleNet,甚至可以忽略AlexNet,但是很难不提及LeNet。LeNet开创性的利用卷积从直接图像中学习特征,在计算性能受限的当时能够节省很多计算量,同时卷积层的使用可以保证图像的空间相关性,最后再使用全连接神经网络进行分类识别。
原始的LeNet是一个5层的卷积神经网络,它主要包括两部分:卷积层块 和 全连接层块,其中卷积层数为2(池化和卷积往往是被算作一层的),全连接层数为3。卷积层块由卷积层加池化层两个这样的基本单位重复堆叠构成。卷积层用来识别图像里的空间模式,如线条和物体局部,之后的最大池化层则用来降低卷积层对位置的敏感性。
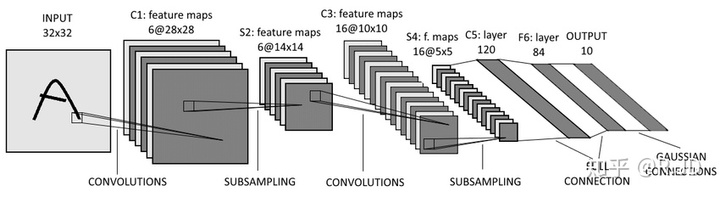
28*28 的灰度图片 如果直接用 DNN来训练的话,全连接层输入为2828=784(weight 也会很大)。LeNet 中卷积层块的输出形状为(通道数 × 高 × 宽),当卷积层块的输出传入全连接层块时,全连接层块会将每个样本变平(flatten)。原来是形状是:(16 × 5 × 5),现在直接变成一个长向量,向量长度为通道数 × 高 × 宽。在本例中,展平后的向量长度为:16 × 5 × 5 = 400。全连接层块含3个全连接层。它们的输出个数分别是120、84和10,其中10为输出的类别个数。PS: 更像是一种变相的全连接,如果把每个 pixel 当成一个 item,input=2828=784 非常deep,现在mlp input 的deep减少了,所以CNN 本质上是在解决参数量这个问题。
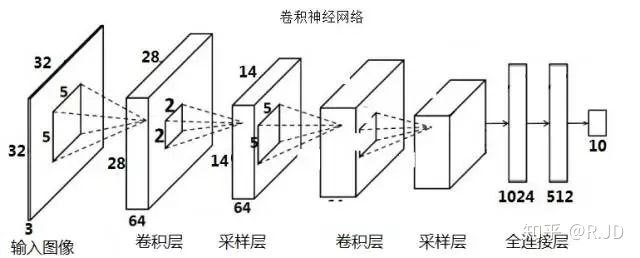
在卷积神经网络,卷积核的数值是未知的,是需要通过“学习”得到的,也就是我们常说的参数。根据不同的卷积核计算出不同的“响应图”,这个“响应图”,就是特征图(feature map)。这就是为什么总是说利用CNN提取图像特征,卷积层的输出就是图像的特征。卷积核的数量关系到特征的丰富性。
https://www.cs.ryerson.ca/~aharley/vis/conv/flat.html 是一个很不错的CNN 2D 动画效果演示。
从 “香农熵” 到 “告警降噪” ,如何提升告警精度? 个人理解:报警也是一个事件序列,根据事件序列计算某一个报警的信息熵(度量事件的重要性)的值,进而实现降噪等效果。比如某个报警 第一次发生 重要性很高,连续报10次 重要性就很低了。
