前言

• 前言
• 整体介绍
  • 逻辑结构
  • 存储结构
• 线性结构
  • 数组和链表
  • 功能函数
  • 滑动窗口
  • 队列
• 树
  • DFS
  • BFS
  • 二叉搜索树
• 图
• 堆
• 一些算法的分析
• 为什么查询和排序是数据结构的基本操作
• 碎碎念
  • 查询的不同意涵
  • 多重查询
  • 设计数据结构的过程是一种“映射”
  • 数据结构与业务设计
• 建模
• 其它

在计算机的世界中，不管实现何种功能或者逻辑，首先都要把功能或者逻辑进行数理化，变成一组特定意义的数据，然后把这组数据结构化、实例化，这是实现功能和逻辑的手段和方法。

《算法通关之路》学习算法像拓扑排序，若没有任何的解题经验，普通人不可能创造一个算法来解决问题。积累经验是十分关键的，当我们积累经验达到一定程度的时候，就可以从新问题中找到旧问题的影子，进一步联想过去所使用的解法，并加以转换，从而解决新问题了。

衡量 CPU 的计算能力：比如一个 Intel 的 i5-2520M @2.5 Ghz 的处理器，则其计算能力 2.5 * 4（4核） = 10 GFLOPS，一个 GFLOPS（gigaFLOPS）等於每秒拾亿（=10^9）次的浮点运算，对于一个O(n^2)复杂度的题目来说， n=2500 就要CPU花1s来计算了。

整体介绍

数据结构分为逻辑结构、存储结构以及对应结构的数据运算，

逻辑结构

数据元素间抽象化的相互关系，与存储无关，比如可以用一个数组表示一个图，也可以用链表存储一个图，或者一个图中包含数组和链表。主要包括：

1. 集合结构中的数据元素之间除了 “同属于一个集合”的关系外，别无其他关系。
2. 线性结构，数据元素之间只存在一对一的关系。⼀般⽽⾔，有前驱和后继的就是线性数据结构。
3. 非线性结构，有了线性结构，我们为什么还需要⾮线性结构呢？ 为了⾼效地兼顾静态操作和动态操作，我们⼀般使⽤树去管理需要⼤量动态操作的 数据。比如平衡⼆叉搜索树的查找和有序数组的⼆分查找本质都是⼀样的，只是数据的存储⽅式不同罢了。那为什么有了有序数组⼆分，还需要⼆叉搜索树呢？原因在于树的结构对于动态数据⽐较友好，⽐如数据是频繁变动的，⽐如经常添加和删除，那么就可以使⽤⼆叉搜索树。
   1. 树形结构结构中的数据元素之间存在一对多的关系。
   2. 图状结构或网状结构结构中的数据元素之间存在多对多的关系。

每种逻辑结构包含一些基本的运算，包括遍历，增减节点等。

存储结构

主要包括：

1. 顺序存储：把逻辑上相邻的元素存储在物理位置上也相邻的存储单元里，元素之间的关系由存储单元的邻接关系来体现。其优点是可以实现随机存取，每个元素占用最少的存储空间；缺点是只能使用相邻的一整块存储单元，因此可能产生较多的外部碎片。
2. 链接存储：不要求逻辑上相邻的元素在物理位置上也相邻，借助指示元素存储地址的指针表示元素之间的逻辑关系。其优点是不会出现碎片现象，充分利用所有存储单元；缺点是每个元素因存储指针而占用额外的存储空间，并且只能实现顺序存取。
3. 索引存储：在存储元素信息的同时，还建立附加的索引表。索引表中的每一项称为索引项，索引项的一般形式是：（关键字，地址）。其优点是检索速度快；缺点是增加了附加的索引表，会占用较多的存储空间。另外，在增加和删除数据时要修改索引表，因而会花费较多的时间。
4. 散列存储：根据元素的关键字直接计算出该元素的存储地址，又称为Hash存储。其优点是检索、增加和删除结点的操作都很快；缺点是如果散列函数不好可能出现元素存储单元的冲突，而解决冲突会增加时间和空间开销。

存储/物理结构通常绕不开寻址问题，以及增删改查的效率问题。我们可以观察到集中存储结构的演进：

1. 顺序存储，直接放在一起
2. 链接存储，数据和位置信息放在一起
3. 索引存储，数据和位置信息完全独立，位置信息存在单独的索引表中。比如磁盘的某些格式
4. 直接寻址表，数据和位置信息完全独立，位置信息存在单独的数组中，数据直接作为数组下标。
5. 哈希表，直接寻址表的改进。

线性结构

数组和链表

各种数据结构，不管是队列，栈等线性数据结构还是树，图的等⾮线性数 据结构，从根本上底层都是数组和链表。不管你⽤的是数组还是链表，⽤ 的都是计算机内存，物理内存是⼀个个⼤⼩相同的内存单元构成的。数组和链表是使⽤物理内存的两种⽅式。PS：同样是存储结构，数组和链表更底层一些

1. 数组是连续的内存空间，通常每⼀个单位的⼤⼩也是固定的，因此可以按下标随机访问。
2. 链表不⼀定连续，⼀般我们是通过⼀个叫 next 指针来遍历查找。链表其实就是⼀个结构体。数据元素的逻辑顺序是通过链表中的指针链接次序实现的。链表由⼀系列结点（链表中每⼀个元素称为结点）组成，结点可以在运⾏时动态⽣成。链表是⼀种递归的数据结构，因此采⽤递归的思想去考虑往往事半功倍。

数组对查询特别友好，对删除和 添加不友好，为了解决这个问题，就有了链表这种数据结构。链表适合 在数据需要有⼀定顺序，但是⼜需要进⾏频繁增删除的场景。

有没有想过为啥只有⼆叉树，⽽没有⼀叉树？实际上链表就是特殊的树，即⼀叉树。单链表只有⼀个后继指针。因此只有前序和后序，没有中序遍历。值得注意的是，前序遍历很容易改造成迭代，为什么呢？前序遍历容易改成不需要栈的递归，⽽后续遍历需要借助栈来完成。由于后续遍历的主逻辑在函数调⽤栈的弹出过程，⽽前序遍历则不需要。

1. 由于链表不⽀持随机访问，因此如果想要获取数组中间项和倒数第⼏项等特定元素就需要⼀些特殊的⼿段，⽽这个⼿段就是快慢指针。⽐如要 找链表中间项就搞两个指针，⼀个⼤步⾛（⼀次⾛两步），⼀个⼩步⾛（⼀次⾛⼀步），这样快指针⾛到头，慢指针刚好在中间。 如果要求链 表倒数第 2 个，那就让快指针先⾛⼀步，慢指针再⾛，这样快指针⾛到头，慢指针刚好在倒数第⼆个。
2. 单链表⽆法在 O(1) 的时间拿到前驱节点，这也是为什么我们遍历的时候⽼是维护⼀个前驱节点的原因。但是本质原因其实是链表的增删操作都依赖前驱节点，这是链表的基本操作，是链表的特性天⽣决定的。
3. 如果要移动单链表的节点，可以使用一个伪头部（dummy head）标记 移动节点后链表的头部。遍历链表时，可以用cur 来标记当前节点。但遍历+移动节点时，cur 本身不能指向待移动的节点，因为cur 会移动，为此要为cur 记录pre，且要记录next = cur.Next以便cur 一会儿指回来。干脆 cur.Next 指向待移动的节点。
4. 在双向链表的实现中，使用一个伪头部（dummy head）和伪尾部（dummy tail）标记界限，这样在添加节点和删除节点的时候就不需要检查相邻的节点是否存在。

功能函数

解决链表问题的时候，先把基本的头插、尾插、遍历、排序（归并法，取中点切分）、反转、找中点、找环等方法备好，结合go 语言的高阶函数，可以大大提高的代码的可读性。比如反转链表，有下面TraverseList 的加持，就比在一个函数里撸业务逻辑 + 遍历逻辑要方便很多，可读性也好很多。

// 插入节点
func InsertAfter(cur, node *ListNode) {
	next := cur.Next
	cur.Next = node
	node.Next = next
}
// 插入list，按list顺序
func InsertAfterByOrder(cur, l *ListNode) {
	next := cur.Next
	TraverseList(l, func(i int, node *ListNode) {
		cur.Next = node
		cur = cur.Next
	})
	cur.Next = next
}
// 插入list，按list 逆序，也就是头插
func InsertAfterByReverseOrder(cur, l *ListNode) {
	next := cur.Next
	TraverseList(l, func(i int, node *ListNode) {
		InsertAfter(cur, node)
	})
	l.Next = next
}
// 此处的 handler 在遍历的过程中还个了node的元信息，即node的索引
func TraverseList(head *ListNode, handler func(i int, node *ListNode)) {
	cur := head
	i := 0
	for cur != nil {
		next := cur.Next // node 可以被handler 挪用
		handler(i, cur)
		i++
		cur = next
	}
}
// 将 list 分为 k 个长度子list 并遍历子list
func TraverseKList(head *ListNode, k int, handler func(head, tail *ListNode, len int)) {
	l := &ListNode{}
	cur := l
	count := 0
	TraverseListByNode(head, func(i int, isTail bool, node *ListNode) {
		cur.Next = node
		cur = cur.Next
		count++
		if (i+1)%k == 0 || isTail {
			handler(l.Next, cur, count)
			l = &ListNode{}
			cur = l
			count = 0
		}
	})
}
func Print(l *ListNode) {
	for l != nil {
		fmt.Println(l.Val)
		l = l.Next
	}
}

滑动窗口

对于数组和字符串来说，除了元素遍历外，还可以遍历连续子序列（滑动窗口），非连续的子序列（xx数之和），元素可以重复多次或无限次的话子序列就更多了（零钱兑换问题）。

func TraverseChildSequence(nums []int, handler func(nums []int, start, end int)) {
	for i := 0; i < len(nums); i++ {
		for j := i; j < len(nums); j++ {
			handler(nums, i, j)
		}
	}
}

在算法优化方面，针对平方阶算法，由于通常必须至少遍历数据一次，无法省略最外层循环，优化重点应考虑是否能降低内层操作的时间复杂度，无论优化到对数阶还是常数阶，算法的效率都会有相当可观的提高。比如i,j 可以认为是滑动窗口的左右指针，但因为j 一定大于i，可以将嵌套的循环展开（正常遍历 子序列/字串 要多层循环），通过减少内层循环的次数来降低算法的时间复杂度，o(n*n) 变为o(n)。

1. 窗口的作用是 排除不可能的解/去除冗余计算，一般来说，固定窗口的某个边界后（左或右），当某个长度的窗口 满足要求或不满足要求时，更长或更短的窗口便不用考虑了，直接考虑下一个固定边界的窗口即可。比如 无重复字符的最长子串pwwkew，当r 探测到第二个w时， 对于l=0，r 再向右探测已经没有意义，此时l 也要向右移，放弃考虑l=0。PS：没有二分这么直接，毕竟二分是O(logn)，窗口是O(n)
2. 窗口长度固定或不固定，左右指针的右移不一定是连续的 ==> 窗口的收缩、扩展、平移。
3. 窗口有整体右移的，可增可减、只增不减、只减不增（从两边最大缩到最小的，比如“乘最多水的容器”）。
   1. 整体右移：本质是遍历数组、字符串的时候，如果[i,j] 不符合要求则不用等j移到右边界就提前右移i，i、j都只会右移不能左移。形象化一点就是，窗口大小可变，但整体在朝右滑动。如果仅靠右移无法解决问题，还要回溯，或者每一次移动后无法继续判断是右移i还是右移j，上面的模板套不上去，就不适合用窗口解决了。
   2. 滑动窗口一般伴随判断函数，判断当前窗口的子序列是否符合要求。判断函数需要辅助的数据结构，比如双端队列（右侧指针右移是加入，左侧指针右移是移除，且保持元素原有的相对顺序）、字典等，记录窗口内元素的特性：比如最大值、最小值、包含某些元素、和等，并与目标进行对比
4. 什么时候用滑动窗口法
   1. 一般来说，滑动窗口法要求解空间有连续的性质，比如子串、连续子序列、xx面积。
   2. 即便题解有连续的性质，也不一定可以用。比如求子序列的最大和，右边是个正数要右移，是个负数也得右移（兴许负数右边的正数更大），右移的终止条件不明确（或者说只能移到右边界才可以终止，此时就退化为暴力遍历了），是否右移跟右侧某个数的正反关系不大。没有「剪枝」加快计算的效果，说明问题在o(n) 时间解决不了，得找o(n^2)的算法了。PS：为什么有的题滑动窗口不可以非得靠dp

滑动窗口法的核心：right 向右移动一步，判断窗⼝内的连续元素是否满⾜限定的条件，如果满足，r 继续右移一步。如果不满足，则右移left 一次或多次，直到窗口内元素满足限定条件。

func TraverseChildSequence(nums []int){
    n := len(nums)
    l := 0
    r := 0
    result := xx

    for r < n {
        seq := nums[l:r]
        //  有时r 右移一步，l 要右移好多步，比如 长度最小的子数组
        for ok := function(seq);ok{    // 判断函数  也可以是 function(nums,l,r)
            result = xx                // 更新一个可行解
            l++                        // 缩小窗口直到不满足条件
        }
        r++                            // 扩大窗口
    }
    return result
}

队列

教科书上一说队列，就是四个字“先进先出”,这四个字是无法表述队列的巨大作用的.

1. 合并请求的一种实现，假设一个方法或类负责管理一个资源,在多线程环境下,这个类便需要”线程安全”
   1. 将这个类改造成线程安全的类
   2. 调整这个类的调用方式.利用生产者消费者模式,所有想要使用这个资源的的线程(生产者)先提交请求到一个队列,由一个专门的线程(消费者)负责接收并处理请求.
2. 轮询的一种实现，假设我们有一个集合，对集合中的元素实现轮询效果。
   1. 我们可以标记一个index，记住上一次使用的元素，进而实现轮询。
   2. 用环形队列存储集合，即天然具备轮询效果。

这两种方式，在多线程环境下，还需注意线程安全问题。

树

DOM 树是⼀种树结构， ⽽ HTML 作为⼀种 DSL 去描述这种树结构的具体表现形式。如果你接触 过 AST，那么 AST 也是⼀种树，XML 也是树结构。

树其实是⼀种特殊的图，是⼀种⽆环连通图，是⼀种极⼤⽆环图，也是⼀种极⼩连通图。

树的遍历分为两种，分别是深度优先遍历和⼴度优先遍历。PS：遍历方法只是用于遍历，不太适用于对树进行删除节点等操作

1. DFS 沿着树的深度遍历树的节点，尽可能深的搜索树的分⽀。 当节点 v 的所在边都⼰被探寻过，搜索将回溯到发现节点 v 的那条边的起 始节点。这⼀过程⼀直进⾏到已发现从源节点可达的所有节点为⽌。如果 还存在未被发现的节点，则选择其中⼀个作为源节点并重复以上过程，整 个进程反复进⾏直到所有节点都被访问为⽌，属于盲⽬搜索。
   1. 树的不同深度优先遍历又分为前中后序。前中后序实际上是指的当前节点相对⼦节点的处理顺序。遍历得从根节点开始访问，然后根据⼦节点指针访问⼦节点，但是 ⼦节点有多个（⼆叉树最多两个）⽅向，所以⼜有了先访问哪个的问题，这造成了不同的遍历⽅式。如果先处理当前 节点再处理⼦节点，那么就是前序。如果先处理左节点，再处理当前节 点，最后处理右节点，就是中序遍历，中序多⽤于⼆叉搜索树，因为⼆叉搜索树的中序遍历是严格 递增的数组。后序遍历⾃然是最后处理当前节点了。
   2. 在第一次遍历到节点时就执行操作，一般只是想遍历执行操作（或输出结果）可选用先序遍历；后续遍历的特点是执行操作时，肯定已经遍历过该节点的左右子节点，故适用于要进行破坏性操作的情况，比如删除所有节点。如果能使用参数 和节点本身的值 来决定应该传递给它的子节点 的参数（给下一层递归传递参数），那么就用前序遍历。如果只有知道子节点的答案，才能计算出当前节点的答案 或应该进行的操作，就用后续遍历。
   3. 从另⼀个⻆度看，树是⼀种递归的数据结构。因此树的遍历算法使⽤递归去完 成⾮常简单，幸运的是树的算法基本上都要依赖于树的遍历。但是递归在计算机中的性能⼀直都有问题，如果你使⽤迭代式⽅ 式去遍历的话，可以借助栈来进⾏，可以极⼤减少代码量。PS：树，递归，栈
   4. DFS 是树的从上到下（操作tree node 跟操作链表差不多），还有从下到上（后序遍历，要借助辅助变量，比如二叉树的最大路径和问题），从左到右遍历。从根到叶子，非根到非叶子，部分子树的左中右路径，最右边的节点（根右左顺序）。PS：真的是只有想不到，没有做不到
2. BFS细分为带层的和不带层的。锯齿形遍历，找每一层的最右节点，每一层的最大值，每一层的平均值。
   1. 层次遍历和 BFS 是完全不⼀样的东⻄，层次遍历就是⼀层层遍历树。层序遍历要求我们区分每一层，也就是返回一个二维数组。而 BFS 的遍历结果是一个一维数组，无法区分每一层。为此层次遍历在每一层遍历开始前，先记录队列中的结点数量 nn（也就是这一层的结点数量），然后一口气处理完这一层的 nn 个结点。
   2. BFS 的核⼼在于求最短问题时候可以提前终⽌，这才是它的核⼼价值， 比如求（无权）最短距离，这个提前终⽌不同于DFS 的剪枝的提前终⽌，⽽是找到最近⽬标的提前终⽌。⽐如我要找距 离最近的⽬标节点，BFS 找到⽬标节点就可以直接返回，⽽ DFS 要穷举 所有可能才能找到最近的。
   3. BFS 采⽤横向搜索的⽅式， 在数据结构上通常采⽤队列结构。

由于链表只有⼀个 next 指针， 因此只有两种遍历。⽽⼆叉树有两个指针，因此常⻅的遍历有三个，除了 前后序，还有⼀个中序。如果是前序遍历，那么你可以想象上⾯的节点都处理好了，怎么处理的不 ⽤管。相应地如果是后序遍历，那么你可以想象下⾯的树都处理好了，怎 么处理的不⽤管。前后序对链表来说⽐较直观。对于树来说，其实更形象地说应该是⾃顶向 下或者⾃底向上。

正常使用一维数组存储一棵二叉树套路是

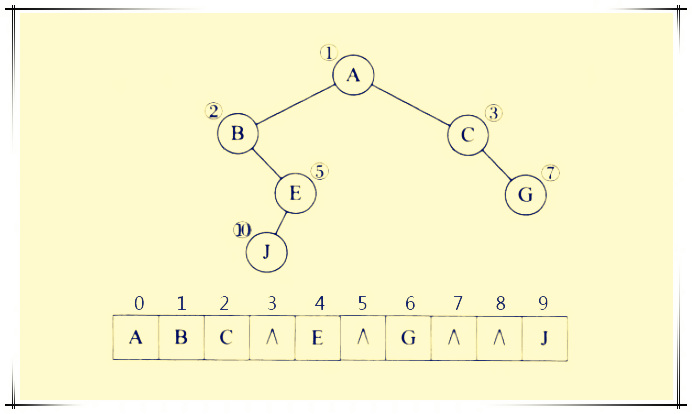
不管是DFS 还是BFS，本质上都是搜索，且通常来说都是暴力搜索（f(n) 展开为f(n-1)，跟暴力搜索差不多了 ），因此需要对问题的所有可能情况进行穷举时，可以使用DFS和BFS，回溯法也是DFS 的一种，即回溯法也是一种保留搜索方法，只不过会涉及前进和回溯的过程。不管是DFS 还是BFS ，如果是在二维矩阵或图上进行搜索，通常都需要使用visited 来记录节点访问状态，树不存在环，也就不需要visited。

DFS

DFS算法流程

1. ⾸先将根节点放⼊stack中。
2. 从stack中取出第⼀个节点，并检验它是否为⽬标。如果找到所有的 节点，则结束搜寻并回传结果。否则将它某⼀个尚未检验过的直接⼦ 节点加⼊stack中。
3. 重复步骤 2。
4. 如果不存在未检测过的直接⼦节点。将上⼀级节点加⼊stack中。 重 复步骤 2。
5. 重复步骤 4。
6. 若stack为空，表示整张图都检查过了——亦即图中没有欲搜寻的⽬标。结束搜寻并回传“找不到⽬标”。

这⾥的 stack 可以理解为⾃⼰实现的栈，也可以理解为“调⽤栈”。如果是“调⽤栈”的时候就是递归，如果是⾃⼰实现的栈的话就是迭代。

⼀个典型的通⽤的 DFS 模板可能是这样的：

const visited = {}  
function dfs(i) {
    if (满⾜特定条件）{
        // 返回结果 or 退出搜索空间
    }
    visited[i] = true       // 将当前状态标为已搜索
    for (根据i能到达的下个状态j) {
        if (!visited[j]) {  // 如果状态j没有被搜索过
            dfs(j)
        }
    }
}

上⾯的 visited 是为了防⽌由于环的存在造成的死循环的。 ⽽我们知道树 是不存在环的，因此树的题⽬⼤多数不需要 visited，因此⼀个树的 DFS 更多是

function dfs(root) {
    if (满⾜特定条件）{
        // 返回结果 or 退出搜索空间
    }
    for (const child of root.children) {
        dfs(child)
    }
}

⽽⼏乎所有的题⽬⼏乎都是⼆叉树，因此下⾯这个模板更常⻅。

function dfs(root) {
    if (满⾜特定条件）{
        // 返回结果 or 退出搜索空间
    }
    dfs(root.left)
    dfs(root.right)
}

其实二叉树的递归遍历，只要包含以上代码，就可以了，而针对不同的题目，我们会设置一些递归的返回值，设计递归函数的参数，或者用外部变量记录的方式，来达到题目的要求。而返回值、参数、外部变量是不影响递归的进行的（只要有以上代码），这时候就是发挥人类智慧，开始设计递归的时候。PS：这段代码有点抛开数据结构 描述算法的味道。数据结构是为算法服务的，算法通常也要建立在某一种或几种数据结构之上。因为没有数据结构直接满足业务问题的需求，所以你可以先假设存在这个数据结构，看看算法怎么做，慢慢剥洋葱，去掉外围、表象，先定义需求再想实现，慢慢跟已有的经验靠拢。面试的时候也可以先定位是哪块的问题，先写模版，再根据问题调整具体逻辑。

// 前序遍历
function dfs(root) {
    if (满⾜特定条件）{
        // 返回结果 or 退出搜索空间
    }
    // 主要逻辑
    dfs(root.left)
    dfs(root.right)
}
// 后序遍历
function dfs(root) {
    if (满⾜特定条件）{
        // 返回结果 or 退出搜索空间
    }
    l = dfs(root.left)
    r = dfs(root.right)
    // 主要逻辑，通常会对l 和r 进行一些操作，比如问题依赖左右子树的返回值，此时应该给dfs 定义返回值
}

树是一个递归结构，因此大部分算法可以先用递归实现，然后看看要求再转为迭代实现。

BFS

本质就是不断访问邻居，把邻居逐个加入队列，根据队列先进先出的特点，把每一层节点访问完后，会继续访问下一层节点。

1. ⾸先将根节点放⼊队列中。
2. 从队列中取出第⼀个节点，并检验它是否为⽬标。 如果找到⽬标，则结束搜索并回传结果。 否则将它所有尚未检验过的直接⼦节点加⼊队列中。
3. 若队列为空，表示整张图都检查过了——亦即图中没有欲搜索的⽬ 标。结束搜索并回传“找不到⽬标”。
4. 重复步骤 2。

const visited = {}
function bfs() {
    let q = new Queue() // 如果在带权图上进行BFS，则可以考虑使用优先级队列来完成
    q.push(初始状态)
    while(q.length) {   // 队列不空，⽣命不⽌
        let i = q.pop()
        if (visited[i]) continue
        if (i 是我们要找的⽬标) return 结果
        for (i的可抵达状态j) {
            if (j 合法) {
                q.push(j)
            }
        }
    }
    return 没找到 
}

二叉搜索树

二叉搜索树的各种花活：查找某个节点（第k小、第k大）；删除[a,b] 范围之外的节点；删除某个节点；校验是否是合法的二叉搜索树；最近公共祖先。

图

深度优先和广度优先遍历，{初始状态，目标状态，规则集合}在寻找最佳策略上的应用，不管你是什么算法，肯定都要遍历的

1. 遍历要考虑几点：树的根，树有几个分叉（先遍历哪个分叉，再遍历哪个分叉），如何记录遍历的结果
2. 不管是哪⼀种遍历， 如果图有环，就⼀定要记录节点的访问情况，防⽌死循环。 DFS 和 BFS 只是⼀种算法思想，不是⼀种具体的算法，因此其有着很强的适应性，⽽不是局限于特点的数据结构的，图 可以⽤，前⾯讲的树也可以⽤（树的前序、中序、后序就是以根节点为起点的 DFS 和 BFS 遍历）。实际上， 只要是⾮线性的数据结构都可以⽤。

DFS 一般用栈实现，BFS 一般用队列实现，可以看看这些算法在工业界的运用，比如BFS 如何应用于跟踪垃圾回收。

岛屿类问题的通用解法、DFS 遍历框架岛屿问题是一类典型的网格问题。每个格子中的数字可能是 0 或者 1。我们把数字为 0 的格子看成海洋格子，数字为 1 的格子看成陆地格子，这样相邻的陆地格子就连接成一个岛屿。在这样一个设定下，就出现了各种岛屿问题的变种，包括岛屿的数量、面积、周长等。不过这些问题，基本都可以用 DFS 遍历来解决。

堆

堆其实就是⼀种数据结构，数据结构是为了算法服务的，那堆这种数据结构是为哪种算法服务的？它的适⽤场景是什么？ 这是每⼀个学习堆的⼈ 第⼀个需要解决的问题。给⼤家⼀个学习建议 - 先不要纠结堆怎么实现的，咱先了解堆解决了什么问题。当你了解了使⽤背景和解决的问题之后，然后当⼀个调包侠，直接⽤现成的堆的 api 解决问题。等你理解得差不多了，再去看堆的原理和实现。

假如你是⼀个排队挂号系统的技术负责⼈。该系统需要给每⼀个前来排队 的⼈发放⼀个排队码（⼊队），并根据先来后到的原则进⾏叫号（出 队）。 除此之外，我们还可以区分了⼏种客户类型， 分别是普通客户， VIP 客 户 和 ⾄尊 VIP 客户。

1. 如果不同的客户使⽤不同的窗⼝的话，我该如何设计实现我的系统？ （⼤家获得的服务不⼀样，⽐如 VIP 客户是专家级医⽣，普通客户是 普通医⽣）
2. 如果不同的客户都使⽤⼀个窗⼝的话，我该如何设计实现我的系统？ （⼤家获得的服务都⼀样，但是优先级不⼀样。⽐如其他条件相同情 况下(⽐如他们都是同时来挂号的)，VIP 客户 优先级⾼于普通客户）

堆的两个核⼼ API 是 push 和 pop。

1. push ： 推⼊⼀个数据，内部怎么组织我不管。对应我上⾯场景⾥ ⾯的排队和插队。
2. pop ： 弹出⼀个数据，该数据⼀定是最⼩的，内部怎么实现我不 管。对应我上⾯场景⾥⾯的叫号。

简单总结下就是，堆就是动态帮你求极值的。当你需要动态求最⼤或最⼩ 值就就⽤它。

堆两种常⻅的实现

1. ⼀种是基于链 表的实现- 跳表。不借助额外空间的情况下，在链表中查找⼀个值，需要按照顺 序⼀个个查找，时间复杂度为 O(N)。我们从链表中每两个元素抽出来，加⼀级索引，⼀级索引指 向了原始链表。如果元素继续增⼤， 继续增加索引的层 数，建⽴⼆级，三级。。。索引，使得链表能够实现⼆分查找，从⽽获得 更好的效率。但是相应地，我们需要付出额外空间的代价。以空间换时间。
2. ⼀种是基于数组的实现 - ⼆叉堆。⼆叉堆就是⼀颗特殊的完全⼆叉树。它的特殊性只体现在⼀ 点，那就是⽗节点的权值不⼤于⼉⼦的权值（⼩顶堆）。那么很⾃然能推导出树 的根节点就是最⼩值。这就起到了堆的取极值的作⽤了。那动态性呢？⼆叉堆是怎么做到的呢？出堆：弹出根节点，使用最右侧节点（数组最后一个元素，方便访问）作为根节点，下沉以便符合堆的性质。 入堆：新节点作为最后一个节点，上浮以便符合堆的性质。
3. 基于红⿊树 的实现。

一些算法的分析

1. ⼆分法的中⼼ - 折半。即⼆分法⽆论如何我们都可以舍弃⼀半解，也就是⽆论如何都可 以将解空间砍半。难点就是：什么条件 和 舍弃哪部分。 找到丢弃元素的原则，这是⼆分法核⼼要解决的问题。⼆分的本质是将问题规模缩⼩到⼀半，因此⼆分和数据结构没有本质关系，但是不同的数据结构却给⼆分赋予了不同的⾊彩。⽐如跳表就是链表的⼆分，⼆叉搜索树就是树的⼆分等。二分是分治思想的体现，分治是分解为几个规模更小的子问题， 直至子问题可以直接求解，二分是直接排除一半。对于最长重复字串问题， 我们可以将原问题拆分为两个子问题，然后在较优的时间复杂度内依次解决它们。
   1. 在 1 到 N 中枚举子串的长度； 对于k（子串长度），如果搜索发现包含重复子串，则增加k值，因为还可能存在更长的子串；如果不包含重复子串，则减小k值，因为不可能有比这更大的了；因为依次加减k效率很低，所以利用二分法操作k值。PS：这个时候，left和right 只是为了计算k，不直接选与选左侧还是选右侧的逻辑。
   2. 对于枚举的长度 L，检查字符串中是否有长度为 L 的重复子串。
   3. 不一定是 f(mid) == target，往往是中间元素和题目的目标值、左右相邻元素以及左右边界元素等存在一定的关联，根据这些关联可以将查找范围缩小一半。
2. 前缀树的核⼼思想是⽤空间换时间，利⽤字符串的公共前缀来降低查询的时间开销。⽐如给你⼀个字符串 query，问你这个字符串是否在字符串集合中出现 过，这样我们就可以将字符串集合建树，建好之后来匹配 query 是否出 现，那有的朋友肯定会问， hashmap 岂不是更好？我们想⼀下⽤百度搜索时候，打个“⼀语”，搜索栏中会给出“⼀语道破”， “⼀语成谶(四声的 chen)”等推荐⽂本，这种叫模糊匹配，也就是给出⼀个模糊的 query，希望给出⼀个相关推荐列表，很明显，hashmap 并不容易做到模糊匹配，⽽ Trie 可以实现基于前缀的模糊搜索。前缀树的 api 主要有以下⼏个：

    insert(word) : 插⼊⼀个单词
    search(word) ：查找⼀个单词是否存在
    startWith(word) ： 查找是否存在以 word 为前缀的单词
   

为什么查询和排序是数据结构的基本操作

以缓存为例，一个缓存（cache）系统主要包含下面这几个操作：

1. 往缓存中添加一个数据
2. 从缓存中删除一个数据
3. 在缓存中查找一个数据

这三个操作都涉及到查找操作，换句话说，对数据的操作无外乎crud，而cud都离不开查询r。进而很明显，基于有序结构的查询速度是最快的，也就引出了排序算法的重要性。PS：查找 ==> 遍历（线性结构是遍历，树形图形结构是回溯） ==> 排序、动态规划、贪心等加速遍历（排序也可以作为预处理的一种手段）==> 分治

1. 查找基本办法是遍历，不同的数据结构不同的遍历方法，迭代、递归（f(n)展开为f(n-1) 也是一种遍历）等等，遍历即暴力搜索，需要利用“搜索目标的特性”在遍历过程中剪枝。一般要充分利用解空间的特性、规律 来加速遍历，有序是规律的一种。
2. 针对不同的数据结构，查找的概念也会泛化。比如图中的查找最短路径，查找数组内符合某个条件的连续子序列（两个指针）/子序列/排列（可以认为是一个多叉树）
3. 遍历的元素类型有多种，遍历可以轮询数据结构的每个节点，也可以是轮询数据结构的每个可能的子结构（比如字符串、数组的子序列）。比如线性表的遍历元素、遍历子串，树的遍历元素、遍历所有路径、遍历所有根到叶子节点路径；一次遍历多个元素（比如双指针、快慢指针）
4. 遍历的方向有多种，从左到右、从右到左、左右一起遍历（比如快排、回文字串），比如树和图的深度优先、广度优先、从左到右、按层从上到下、从下到上。比如遍历子串，可以i、j分别代表子串的头尾，也可以使用l、i分别代表子串的长度和起始的位置。
5. 查找/遍历有多种目的，遍历的过程中找到符合某个条件的节点等等。解空间元素之间的关系，比如两个相等的子序列。遍历可能操作数据，比如把一个数通过限定操作变为1。
6. 复杂结构的排序比较少见，排序一般可以加速单重遍历（毕竟不用一个个找了），对于子序列/排列问题，涉及到多重遍历（层数由子序列/排列的长度决定），有时根据“搜索目标的特性”，多重遍历的部分层遍历可以是并列关系（比如结果元素不重复且此消彼长，“三数之和+结果不重复”问题，可以使用头尾指针分别从头尾开始遍历，一层当两层用），因此排序也可以减少多重遍历的层数。

整体脉络：数据结构 ==> 增删改查、遍历方法 ==> 基于基本方法之上的，找到符合某一个/多个特征的元素 的算法 ==> 加速遍历。

从解空间的视角看：

1. 一般需要暴力法先列出所有解空间，解空间的描述很多样：窗口、树、二维表格（乘水最多的容器）等。
2. 解空间的分解也有先后，比如求一个字符串S的最长重复子序列，在S的所有子串中找到两个相等的、最长的。你可以先看S1开头的子串有没有重复的，再看S2的….。也可以先查询是否存在长度为len(S)的子串，然后再看长度为len(S)-1的子串…。区别是后者可以“剪枝”，因为如果能找到 长度为k的重复子串，那么k-1的就不用考虑了。
3. 遍历的过程一般伴随有判断（实现时一般抽出来作为一个函数）的过程，比如是不是两数之和，是不是最长回文子串等
4. 解空间的遍历
   1. 是依次遍历(for i:=0;i<len;i++{...})，从左到右，从中间到两边，如果解空间是矩阵的话，从哪个角开始。还是取一些巧，二分遍历、跳跃着遍历（知道了当前步骤的结构，下一步或几步明显不符合结果），
   2. 是否可以直接通过当前步算出来而无需调用判断函数（本质就是动态规划，有重复子问题）。脉络是时间复杂度从低到高：先试试O(logn)（二分），不行再试试O(n)(滑动窗口)，实在不行O(n^2)，此时遍历可以是暴力的，可以继续试试能不能减少判断函数的执行（动态规划，状态转移公式），实在不行就分治（无重复子问题）。
5. 很多思路就是从暴力法来的，从笨方法优化而来，这是最稳妥的。暴力法不需要想思路，是你解答所有问题的思维起点，就是遍历所有可能，判断其是否是解，而不是去拼凑一个解。你直接想一个精巧的方法， 很可能不符合所有情况。很多思路都是优化中得到的思路，最后再冠以一个合理的解释，我们要是直接学了这些解释，很容易就碰到具体的问题又忘了。PS：这也是为什么《算法通关之路》不厌其烦的每道题先讲一下暴力法。
6. 暴力法之所以有问题，一方面是因为它产生重复的计算；另一方面暴力法往往还会去执行一些根本不可能是结果的代码。可以通过辅助数据结构、剪枝、滑动窗口来优化。注意，你要砍掉的是不可能是结果的遍历，而不是想办法去拼凑解，因为你总是很难罗列所有情况。PS：字节一面算法题的教训

既然排序，就得有容器。排序排序，得有个容器，把东西放里面排排放，那才有顺序的概念。于是就有了 “容器” 的概念。为了操作容器，就要对容器进行更高程度的抽象，于是就有了 “迭代器”的概念。迭代器，就是用来访问容器里存储的对象的。是容器的抓手。

碎碎念

查询的不同意涵

数据结构，model the application data，it is generally a requirement for any application to insert, edit and query a data store. Data structures offer different ways to store data items, while the algorithms provide techniques for managing this data. 不管什么样的数据结构，都跑不掉insert、edit、和query。尤其是query ，对于不同的数据结构，意涵很丰富

1. 查询的入参不同，可能是index、数据的某个属性、范围、数据的某个特征（比如第k大的数）
2. 查询返回的结果不同，可能是数据本身、数据集合、也可能是多个数据的组合（比如图的最优路径）

多重查询

1. 数组 + hash 构成了散列表，根据index 查询和 key 查询 都是O(1)
2. 假设 既想根据学号 又想根据成绩 查询学生，则可以先按学号递增组织学生数据，再按照分数构造一个散列表（该思想对应到数据库上，就是针对主键另外建了一个非聚簇索引）。

为什么散列表和链表经常会一起使用？

1. 链表只能基于一个维度来构建有序数据，也只能基于这个维度来查询数据。基于链表构建一个散列表 则相当于 构建了一个“非聚簇索引”，增加了查询维度。
2. 散列表中数据是经过散列函数打乱之后无规律存储的，在散列表上加链表（使用指针将散列表的n 个拉链 串起来），则可以支持散列表按照插入或访问顺序遍历数据，比如java中的LinkedHashMap。

设计数据结构的过程是一种“映射”

Data StructureComputer solution of a real-world problem involves designing some ideal data structures, and then mapping these onto available data structures (e.g. arrays, records, lists, queues, and trees) for the implementation. 先假设存在一种理想结构（以及它的api是啥，具体的说输入输出是啥），用流程 + 数据结构 将问题解决，然后再考虑着 组合基本结构去实现。

我们说面向的对象的四个基本特性：抽象、封装、继承、多态。在四个基本特性之上呢，一群类的组合，有了各种设计模式。

数组 + 哈希函数 就成了一个散列表。 也就是 基本特性的组合，是否也有设计模式一说呢？ 对于跳表来说，与其说数据结构本来就是那样子，还不如说为了在链表上提高查询速度而衍生的数据结构。亦或者说B+树，我们也可以说先有底层那一条叶子链，再有的上层索引结构。

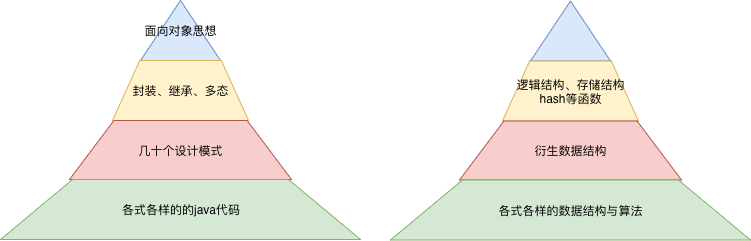
数据结构与业务设计

一般的业务系统要建立数据库表，数据库表要建立索引。笔者有一个经验，不要一开始建立索引。而是业务代码完毕后，观察常查询的属性，然后对这些数据建立索引。如果你愿意，索引 + 数据库表，就是一种数据结构，数据结构的构建（比如建立索引） 要反应业务的“意志”。

Definition of a Data Structure & AlgorithmsComputing applications use many different types of data. Some applications model data within database systems, in which case the database system handles the details of choosing data structures, as well as the algorithms to manage them. However, in many cases, applications model their own data. When programmers decide what type of data structure to use for a particular set of data in an application, they need to take into account the specific data items to be stored, the relationships between data items and how the data will be accessed from within the application logic. ddd(一)——领域驱动理念入门 也提到，一般业务以数据库ER设计为驱动，数据库设计代表了对业务的认识深度，也是业务的精华所在。 由此看， 数据库完成了一个项目本身应有的数据结构与算法的活儿，我们不用直接进行数据结构设计（这由数据库封装），而是通过ER表设计来间接影响数据库进行实际的数据结构设计。

Algorithms for managing data structures sometimes involve recursion. With recursion, an algorithm calls itself, which means it repeats its own processes as part of a looping structure, with each step simplifying the problem at hand. Recursive algorithms can allow programmers to implement efficient sorting and searching techniques within their applications. However, writing recursive algorithms can be difficult for beginners, as it does require a significant amount of practice. 这段有一个很有意义的观点，Recursive algorithms 一般要对应 looping structure，是不是可以笼统的说：递归的算法一般对应着可以递归的数据结构。

建模

数据结构 + 数据结构 ==> 某方面更优秀的数据结构。算法也要类似的特点，计算机只能执行：顺序；循环；选择。leetcode上成千上万道算法题，最后只归结到十几类题目，比如“排序+自定义排序策略”，就可以解决很多实际问题。数据结构 + 算法 ==> 更优秀的数据结构。

基于冯诺依曼体系结构的计算机本质上是一个状态机，为什么这么说呢？因为 CPU 要进行计算就必须和内存打交道。内存就是用来保存状态（数据）的，内存中当前存储的所有数据构成了当前的状态，CPU 只能利用当前的状态计算下一个状态。我们用计算机处理问题，无非就是在思考：如何用变量来储存状态，以及如何在状态之间转移：由一些变量计算出另一些变量，由当前状态计算出下一状态。基于这些，我们也就得到了评判算法的优劣最主要的两个指标：

1. 空间复杂度：就是为了支持计算所必需存储的状态
2. 时间复杂度：就是初始状态到最终状态所需多少步

有两个容量分别为x升和y升的水壶及无限多的水，请判断能够通过使用这两个水壶，得到恰好z升的水？如果可以，请用以上水壶中的一或两个来盛放取得的z升水。允许你：装满任意一个水壶/清空任意一个水壶/从一个水壶向另一个水壶倒水，直到装满或倒空。

我们用(x,y)这样的元组来表示水壶的盛水状态，那么初始状态就是(0,0)，可以采取的行动有以下6种。

1. 将x的水倒空
2. 将y的水倒空
3. 将x的水盛满
4. 将y的水盛满
5. 将x的水全部倒给y（x可能倒不完，同时y可能溢出）
6. 将y的水全部倒给x（y可能倒不完，同时x可能溢出） 每一种行动之后，都对应一个状态，同样元组表示。

描述解空间 ==> 在解空间中搜索/查找（基础是遍历） ==> 复杂数据结构与算法 ==> 基本数据结构 + 顺序；循环；选择

其它

数据结构的”基本类型化”：较早出现的编程语言，比如c语言，基本类型只包括:int,char,long等，string、map等则需要引用库。而对于新兴语言，比如go和python等，则在语言层面支持string、map等复杂结构。这一趋势，甚至扩展到了一些内存数据库。

算法题的面试其实是比自己做题要来得简单的，因为有面试官的帮忙，大部分情况下还不用bug free通过所有测试用例，只需要写个代码思路就可以，而思路在某些情况下还是面试官给的。算法问答的核心是多跟面试官沟通。