简介
- 简介
- 从训练机器人行走开始
- 什么是强化学习
- 强化学习的数学建模基础
- 分类
- Policy Gradient(策略梯度)
- actor-critic
- 总结一下
- online/offline policy
- 缺点
- 其它
强化学习的目标是找到一个「策略」,所谓策略,就是「在某个环境状态下,需要采取某个动作」。这里的「学习」二字,可以借由「机器学习」的概念去理解,你可以笼统地认为为是「用一个函数去逼近这个策略」。而「神经网络」就可以看做是这个函数逼近器。而「强化」二字,可以借由「控制系统」的概念去理解,RL 算法是构建一个「闭环控制系统」,其目标是通过与环境的交互来优化决策。在不断地「采样-评估-更新」过程中,找到或逼近解一个高维动态规划问题的「最优策略」,其本质是求解由随机过程和不完全信息耦合所带来的高维优化问题。在这个视角下,RL的数学本质可以概括为:构建闭环的学习系统,利用反馈信息去逼近策略函数。PS:「闭环」是控制系统中的概念,具有反馈环节,能够感知系统输出的变化,并根据输出的变化进行调整。与之相对的是「开环」概念,没有反馈环节。
PS:单单是rl 强化学习本身的推导就是一门很厚的知识,搞明白actor-critic 就有百分之七八十了,之后是ppo 针对actor-critic 的一些调整,可以直接看PPO理论推导+代码实战
从训练机器人行走开始
策略梯度法入门—强化学习该例是要设计一个两腿机器人,使其能自动的行走。机器人左右腿的跨、膝、踝共有6个关节,都装有小电机,希望能自动控制它的6个小电机,使机器人能和人一样正常的行走。
强化学习需要一个软件系统,其基本组成包括:
- 代理(Agent智能体):是个软件,相当于机器人的大脑,是强化学习的核心。它可以接受环境状态的信息,还可以将计算的结果传输给环境。其中,负责计算的是个函数,称作策略(policy),是强化学习最重要的部分。
-
环境(Environment):代理以外的部分都是环境。和通常的环境概念不同,机器人所处的周边当然是环境,不同的是,机器人的躯体四肢都在代理之外,也都归于环境,比如躯干的高度,各个腿及各个关节的位置、速度等。此例中,环境状态使用31个观测值。包括
- 躯干沿Y和Z轴方向的坐标值,
- 躯干沿X、Y和Z方向的速度,
- 躯干旋转的角度和角速度,
- 6个关节的角度和角速度,
- 脚和地面之间的接触力。
- 状态(State):指环境的状态。机器人一直在移动,所以,周围环境的状态,以及自身各关节的状态也在不断的变化。
- 行动(Action):指代理根据当前状态采取的动作,比如机器人向左或向右,向前或向后移动等。
- 奖励(Reward):代理在当前状态下,采取了某个行动之后,会获得环境的反馈,称作奖励。但可能是奖励,也可能是惩罚,实际是代理对行动的评价。在强化学习中,奖励非常重要,因为样本没有标签,所以奖励起到引领学习的作用。
使机器人正常行走要做的工作。让两腿机器人正常行走,要做的工作是,用正确的指令控制每个关节,使机器人的腿和躯干正确的移动,这需要有六个关节的扭矩指令。在给定的环境状态下,如何得到正确的指令,这就是强化学习要做的工作。用传统方法开发机器人的行走程序,要人工设计逻辑、循环、控制器及参数等等,需要很多的环路,非常复杂。而强化学习的思想极为简单,它不考虑整个过程的具体步骤,不进行一步步的具体设计,而是把这一切复杂工作都塞到一个函数里,这个函数称作策略函数。策略收到环境传来的31个状态值,会自动计算出6个可供执行的指令,指令正确,机器人就会正常的行走。可以看出,强化学习中,机器人能正常行走的关键,就是这个策略函数。
所以下面的重点是:智能体里的策略函数是什么形式?它如何进行学习?如何通过环境状态值计算出6个正确的指令,使机器人能正常的行走。
- 策略是个函数,因其过于复杂,很难用显性的公式来表式。对于这种连续且复杂的问题,强化学习是采用功能强大的神经网络来近似这个函数。这里策略神经网络是用的多层感知机(最基本的前馈神经网络),并以此为例进行说明。
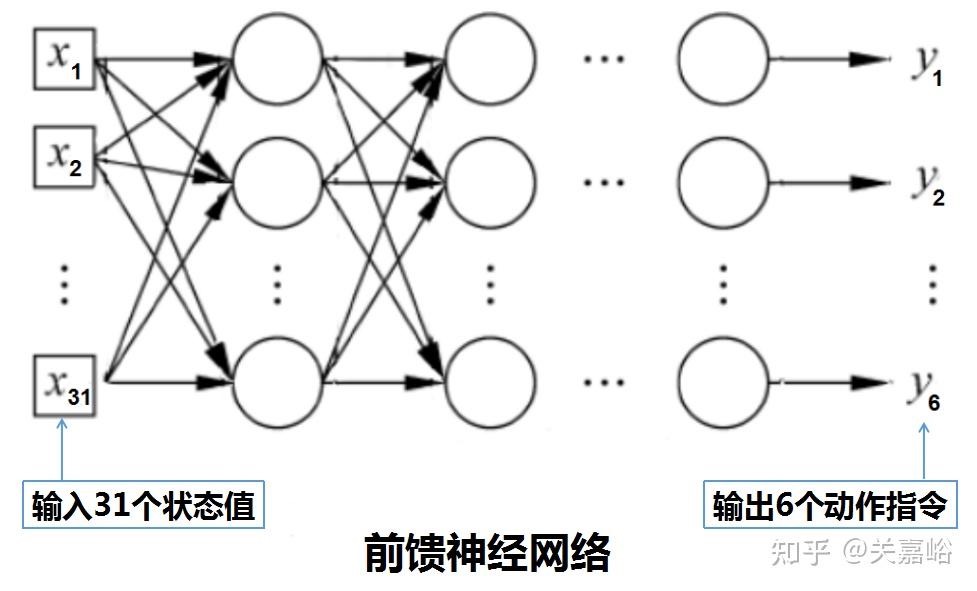 神经网络包含多个隐藏层,每层都有数百个神经元,没有足够多的神经元,网络无法拟合这么复杂的非线性函数,不可能将31个观察值正确的映射到6个动作。但是,神经元过多,将花费更多的时间训练,还容易得到过拟合的逻辑。所以,如何选择网络结构,包括网络层的数量,各层如何连接,以及每层神经元的数量等等,需要丰富的经验和知识找到最佳平衡点,使训练即可行又有效。
神经网络包含多个隐藏层,每层都有数百个神经元,没有足够多的神经元,网络无法拟合这么复杂的非线性函数,不可能将31个观察值正确的映射到6个动作。但是,神经元过多,将花费更多的时间训练,还容易得到过拟合的逻辑。所以,如何选择网络结构,包括网络层的数量,各层如何连接,以及每层神经元的数量等等,需要丰富的经验和知识找到最佳平衡点,使训练即可行又有效。 - 神经网络的学习过程。策略函数的学习过程,可以选择仿真或真实行走的方式。方法是让机器人不断的行走,不断的调整策略函数里的参数w和b,直至得到能使机器人正常行走的网络模型(策略函数)。一般前馈网络的学习,样本都有标签(标准答案),在一次前向传播后,计算出结果,先求计算结果与标签的误差(损失函数),再求损失函数对各个节点的偏导数(梯度),然后求出损失函数对各个参数w和b的偏导数,用这些参数的偏导数来调整各个参数。但是,强化学习是以状态观测值作为输入(样本),没有标签,当然也就没有损失函数,那么求谁的梯度(偏导数)?没有梯度怎么修改参数w和b?强化学习的作法是设计一个奖励函数,用动作的奖励函数作准则,来调整网络的参数。强化学习里奖励函数的作用,相当于一般神经网络里的损失函数。做法是,每输入31个环境状态值,用策略函数计算出6个动作指令,然后执行这6个动作指令,当然这会改变了环境的状态值,包括躯干和6个关节的位置和速度等,然后再计算这个动作的奖励函数值,通过提高奖励函数值来调整网络的各个参数w和b。注意,不是像一般前馈网络学习那样,通过减小损失函数来调整参数w和b。
- 奖励函数。奖励函数是人工精心设计的,其作用相当于前馈网络或循环网络的标签,是引导机器人正常行走的根据。此例已经设计好的奖励函数是$ r_t = v_x -3y^2 - 50z^2 + 25xx - 0.22xx $,其中 $v_x$ 是前进速度,$v_x$ 越大,机器人走得越快。y是侧向位移,使机器人沿着一条直线移动,不向左右偏移,越小越好。z是机器人重心的垂直位移,是要机器人的躯干保持一定的高度,不摔倒、不跳跃或蹲着走路,越小越好。其余设置,这里不逐一深究。总之,这个奖励函数值越大,机器人走的就越好。奖励函数非常重要,但其设置是个难点,需要丰富的经验和专业知识。
- 策略函数的学习过程。现在,策略函数是一个神经网络(多层感知机),策略能否做出正确的动作指令,取决于网络里的所有参数w和b。而评价一个动作优劣的标准,是这个动作的奖励函数,奖励函数的值越高,该动作就越好。所以,强化学习是求出奖励函数对各个参数w和b的梯度,让参数w和b沿着奖励函数的梯度方向调整,这样奖励函数值就会升高,下一次遇到同样的环境状态,策略计算出的指令就会更好。就这样,反复的调整参数w和b,最终得到一个可以时时做出正确指令的神经网络。
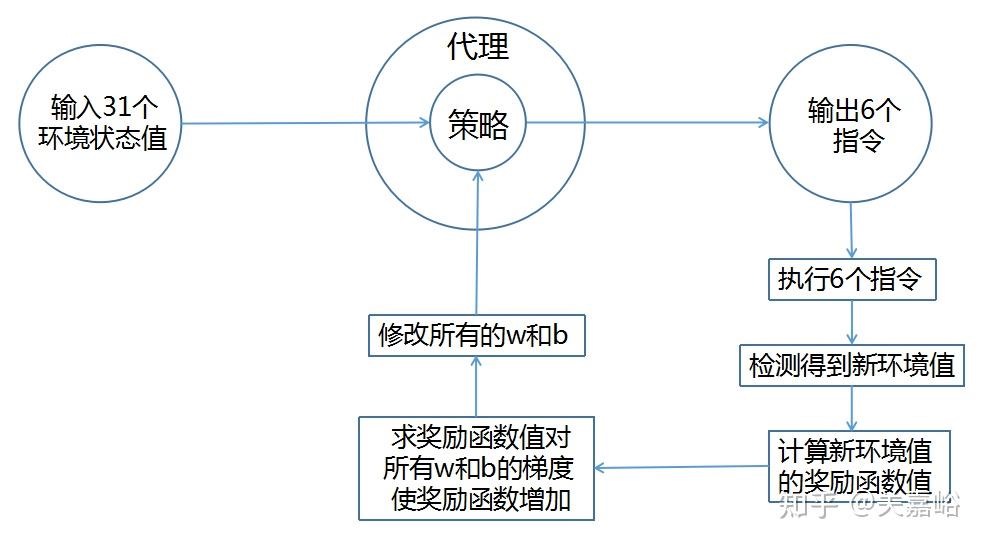 具体作法大意是
具体作法大意是
- 输入31个环境值;
- 网络计算得到6个指令,执行指令改变了环境,检 测得到了31个新环境值;
- 用检测到的31个新环境值,求奖励函数对各个参数w和b的梯度(偏导数),即反向传播;
- 修改网络所有的参数w和b;
- 返回到1,进行下一循环学习。 就这样,代理不断与环境交互,不断修改策略的参数,最终,在任何状态情况下,它都会采取最有利的行动。强化学习的过程,就是不断优化这个策略的过程,整个过程,是计算机自己在学习正确的参数,实际是个反复优化完善网络的过程。上述2执行6个指令后得到的新环境状态值,是环境检测出来的,和策略网络没有连在一起,用它求奖励函数值没问题,直接代入就行。但用这个新环境状态值对各个参数w和b求偏导数,就有问题了,因为它和策略网络根本没连接上。
PS: rl和dl都是在想办法,算一个loss,优化w和b。 李宏毅老师提到 ml 约等于looking for a funtion, 对监督学习 label = func(input), 对rl来说,action=func(observation)。
什么是强化学习
众多表述
- 强化学习(Reinforcement Learning, RL)是一种机器学习方法,模型通过与环境的交互来学习决策策略(a method to find a policy with high rewards)。模型在每一步的选择中会得到奖励或惩罚,目标是最大化长期的累积奖励。在自然语言处理(NLP)中,强化学习可以用于优化模型的输出,使其更符合期望的目标。强化学习算法主要以原来的训练结果为基础,只是不断调整新的处理结果与目标问题(强化学习算法本身的专业术语叫“环境”)之间的偏差(专业术语叫“奖励”)。
- RL包含行动、 环境、观察、奖励机制等模块,奖励机制是RL 具有特色的模块,在奖励机制出现之前,众多机器学习算法是通过损失函数的梯度更新来进行模型学习的,这种损失函数优化效果带来的是模型直接收益反馈,然而不同于传统机器学习任务的单一任务分析,针对复杂环境的分析以及任意动作的带来的奖励反馈极为动态,比如我们在驾驶场景,方向盘多转动5度所带来的奖励收益是极为复杂的,这也让众多传统机器学习算法无法对上述任务进行建模。如何设计良好的奖励机制,是强化学习系统算法建模之前就要想清楚的问题。RLHF的做法是不再像原有RL依赖机器计算奖励反馈,而是利用人工计算奖励反馈,所以该算法框架才被定义为基于人类反馈的强化学习框架。
- 强化学习是一种机器学习方法,它通过让智能体在环境中执行动作,以获得反馈或奖励信号,从而学习最优策略。通过不断地试错和调整策略,智能体逐渐找到能够最大化长期回报的行为路径。这种学习方法常用于需要决策和动态环境交互的任务,如游戏、机器人导航和自动化控制系统。想象一下,你有一只机器狗,它已经在基本的狗行为上进行了初步训练,比如行走和听从简单的命令。
- 微调就像是对这只机器狗进行进一步的训练以适应特定的任务环境。比如说,你希望这只机器狗能够在公园里捡回特定种类的球。通过微调,你可以在原有的训练基础上,用一组特定的数据集(比如各种颜色和大小的球)来调整其行为,使其在新环境中表现得更好。
- 强化学习训练则有点像是教这只机器狗通过尝试和错误来学习新技能(通常不依赖于预定义的数据集,而是依赖于与环境的持续交互。)。在这种情况下,你没有直接告诉它应该怎么做,而是为它设定一个目标,比如尽可能快地找到并捡起一只球。机器狗每完成一次任务都会获得奖励,然后它将通过调整自己的行为来最大化获得的奖励。例如,如果机器狗发现跑直线能更快地找到球,它可能会在未来的尝试中更倾向于这样做。
- 强化学习是一种植根于试错学习(Trial-and-error learning)思想的智能化方法,其核心逻辑是通过与环境的持续交互不断优化系统决策能力。“强化”这一概念的起源可追溯至 1927 年,最初被用于描述巴甫洛夫条件反射实验中动物行为模式的增强现象。直到 20 世纪 60 年代,“强化”及“强化学习”等术语才正式进入工程领域,被用于定义基于试错机制的学习方法。进入 20 世纪 80 年代,强化学习算法迎来关键突破——在马尔可夫决策过程(Markov Decision Processes,MDP)框架下逐步构建起相对严谨的数学理论基础,为技术的规范化发展奠定了核心支撑,并在实际应用中开始展现突破性价值。
o1核心作者MIT演讲:激励AI自我学习,比试图教会AI每一项任务更重要
- 激励AI自我学习比试图教会AI每一项具体任务更重要。如果尝试以尽可能少的努力解决数十个任务,那么单独模式识别每个任务可能是最简单的;如果尝试解决数万亿个任务,通过学习通用技能(例如语言、推理等)可能会更容易解决它们。“授人以鱼不如授人以渔”,用一种基于激励的方法来解决任务。Teach him the taste of fish and make him hungry.(教AI尝尝鱼的味道,让他饿一下)然后AI就会自己出去钓鱼,在此过程中,AI将学习其他技能,例如耐心、学习阅读天气、了解鱼等。其中一些技能是通用的,可以应用于其他任务。面对这一“循循善诱”的过程,也许有人认为还不如直接教来得快。但在Hyung Won看来:对于人类来说确实如此,但是对于机器来说,我们可以提供更多的计算来缩短时间。换句话说,面对有限的时间,人类也许还要在专家 or 通才之间做选择,但对于机器来说,算力就能出奇迹。
- 此外,他还认为当前存在一个误区,即人们正在试图让AI学会像人类一样思考。但问题是,我们并不知道自己在神经元层面是如何思考的。机器应该有更多的自主性来选择如何学习,而不是被限制在人类理解的数学语言和结构中。在他看来,一个系统或算法过于依赖人为设定的规则和结构,那么它可能难以适应新的、未预见的情况或数据。造成的结果就是,面对更大规模或更复杂的问题时,其扩展能力将会受限。
PPO理论推导+代码实战 建议细读。
强化学习整体流程
- 强化学习的两个实体:智能体(Agent/Actor)与环境(Environment)。在强化学习中,学习和决策者称为智能体(Agent),智能体之外所有与其相互作用的事物称为环境。
- 强化学习的核心在于两个实体的交互:
- 状态空间S:S即为State,指环境中所有可能状态的集合
- 动作空间A:A即为Action,指智能体所有可能动作的集合
- 奖励R:R即为Reward,指智能体在环境的某一状态下所获得的奖励,scalar for each step or episode。episode 指的是智能体(agent)从环境(environment)中 开始交互到结束的一段完整轨迹,这段轨迹由一系列状态(state)、动作(action)、奖励(reward)组成:$s_0, a_0, r_1, s_1, a_1, r_2, …, s_T$,其中 T 表示 episode 结束的时间步(终止状态)。
如何学习
Agent learns to take action to maximize expected reward.单从rl训练来说,与supervised learning也是分三步:function with unknown variable; define loss from training data; optimization.
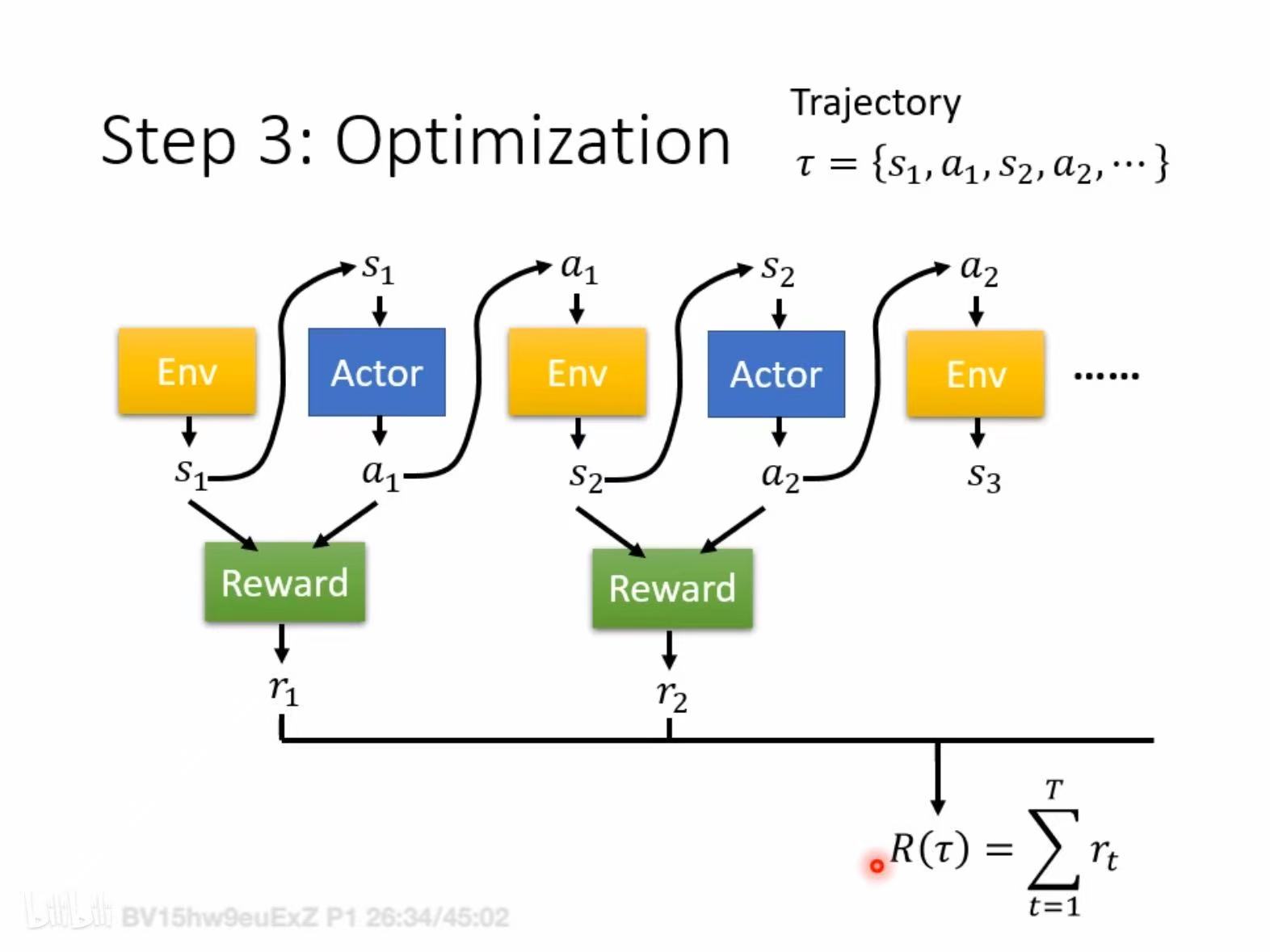
无监督学习直接基于给定的数据进行建模,其主要目标是发现数据中隐藏的内在结构或模式,整个过程没有外部反馈,算法自行探索静态数据。而强化学习则不同,它通过与环境的持续交互来学习,智能体通过试错不断调整策略,以最大化累积奖励(return = $\sum_{t=1}^{T}r_t$)。也就是如果你能收集很多<s,a->r> training data, 就可以监督学习Agent(如果agent 是一个network的话),不过一般不直接用r,我们用A来表示你有多希望s时采取动作a,<s,a->A>,在实践中,A有多种表示方式。
- r 直接作为A,缺点是会导致actor 比较短视
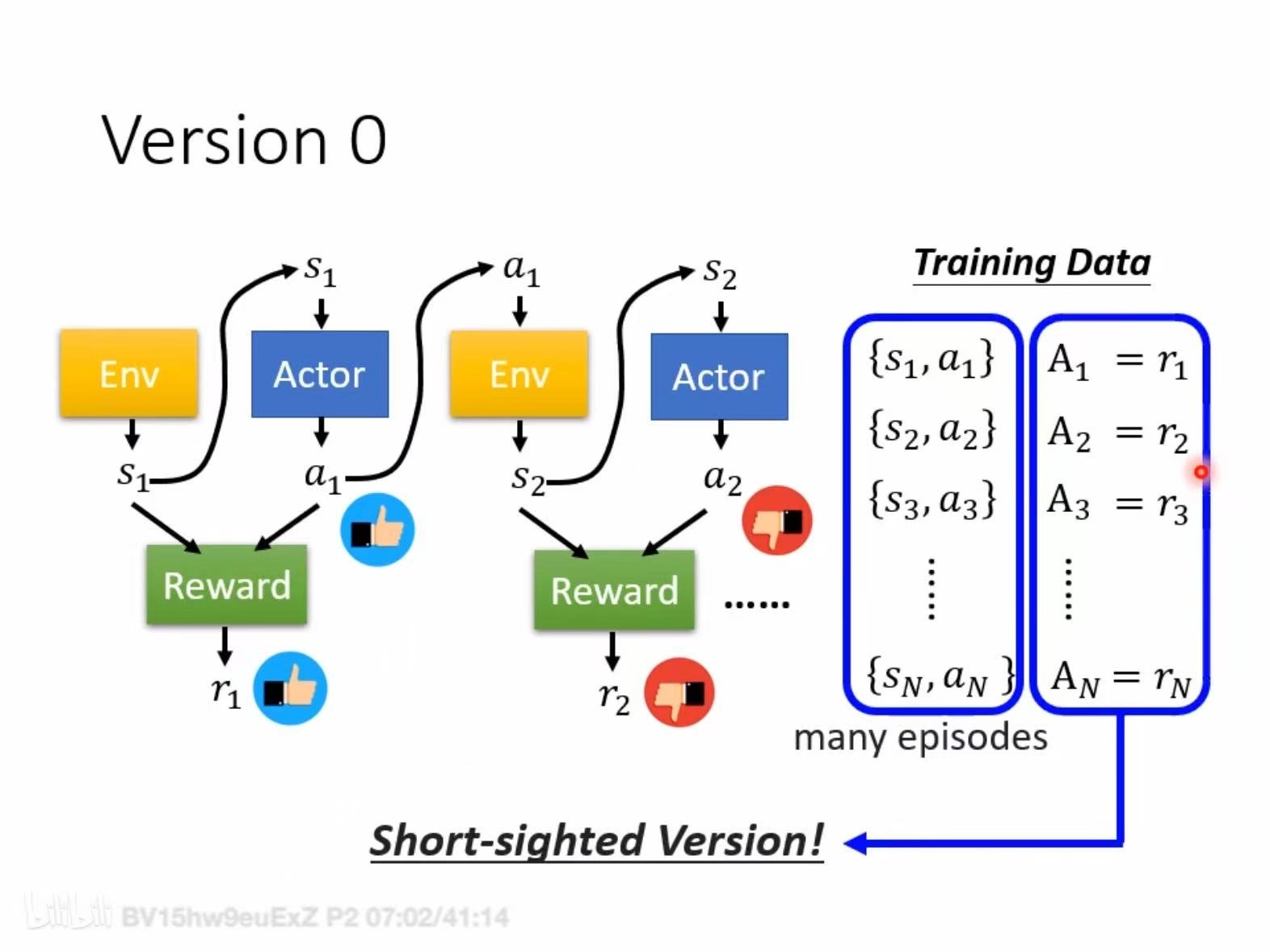
- G 作为A,缺点是越靠前的a的A越大,也不符合实际。
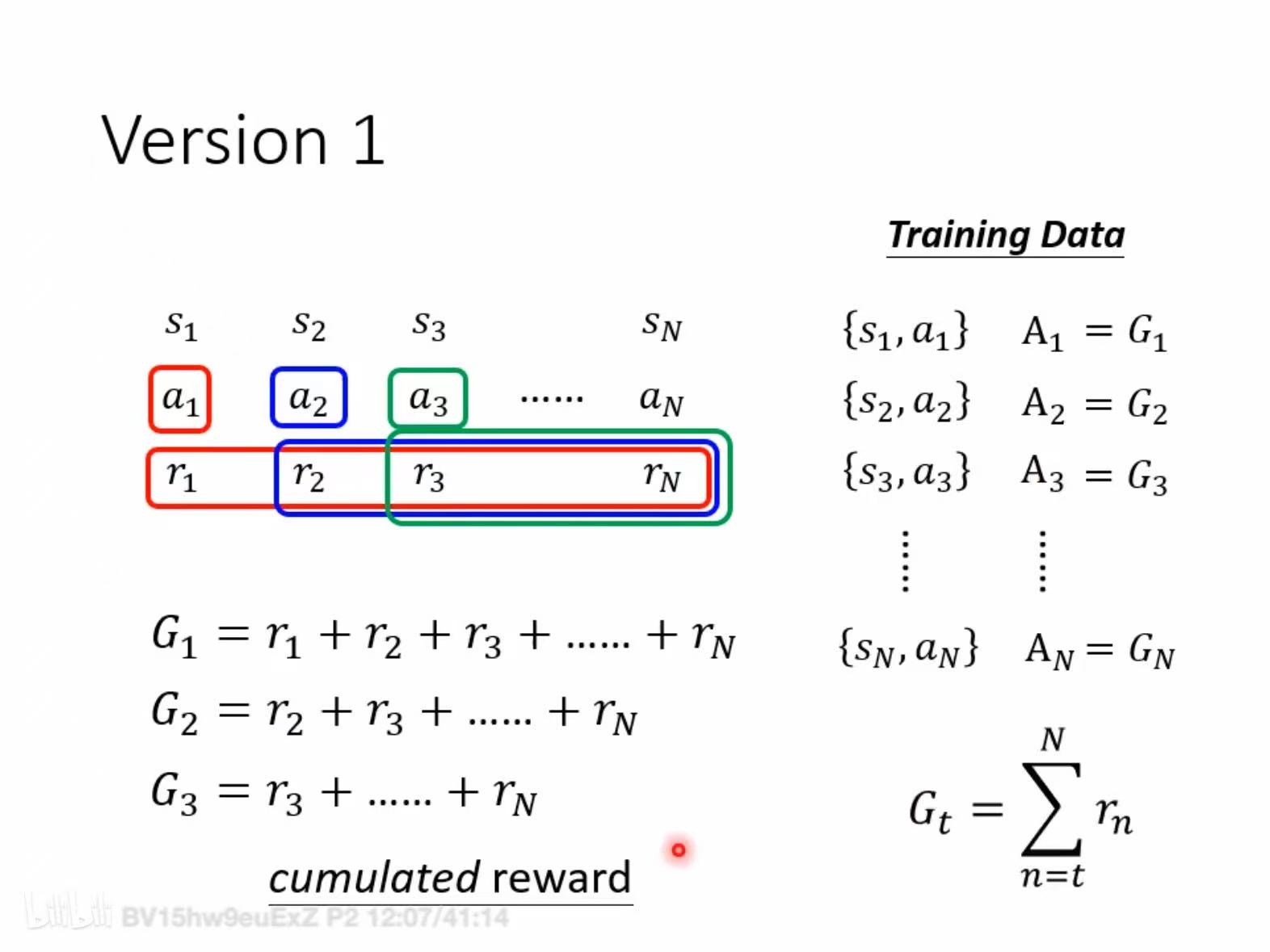
- 离a越远的r打一下折扣

- G是绝对值,不能直接用,比如一次考试你单说考了80分其实说不清楚你考的好与差,所以要对G标准化一下,一个简单的方法是减去一个baseline。,但如何选baseline也有很多花样了(下文会考)。

- 但其实这么做还有问题,比如对于下围棋来说,大部分a的$r_i$都是0,最后最后一步的a的r是1(赢)或-1(输)。所以A的花活很多,甚至专门安排一个模型来学习。
强化学习的数学建模基础
强化学习的学习过程通常被建模为马尔可夫决策过程(Markov Decision Process,MDP)。它有个重要特性:下一个时刻的状态只取决于当前状态,与过去状态无关。
- 你可能听说过马尔可夫随机过程(stochastic process),用数学公式表示就是:
P(St+1∣St)=P(St+1∣S1,...,St)。- 随机过程(stochastic process)是概率论的“动力学”部分。概率论的研究对象是静态的随机现象,而随机过程的研究对象是随时间演变的随机现象(例如气温随时间的变化)。在随机过程中,随机现象在某时刻 t 的取值是一个随机向量,用 St 表示,所有可能的状态组成状态集合 S。随机现象便是状态的变化过程。在某时刻 t 的状态 St 通常取决于 t 时刻之前的状态。我们将已知历史信息
(S1,S2,...,St)时,下一时刻状态为 St+1 的概率表示成P(St+1∣S1,S2,...,St)。 - 当且仅当某时刻的状态只取决于上一时刻的状态时,一个随机过程被称为具有马尔可夫性质,用公式表示为
P(St+1∣St)=P(St+1∣S1,S2,...,St)。也就是说,当前状态是未来的充分统计量,即下一个状态只取决于当前状态,而不会受到过去状态的影响。例如:下棋时,当前棋盘状态已包含所有历史走棋信息,无需记忆每一步的落子顺序。只要当前状态可知,所有的历史信息都不再需要了,利用当前状态信息就可以决策未来。
- 随机过程(stochastic process)是概率论的“动力学”部分。概率论的研究对象是静态的随机现象,而随机过程的研究对象是随时间演变的随机现象(例如气温随时间的变化)。在随机过程中,随机现象在某时刻 t 的取值是一个随机向量,用 St 表示,所有可能的状态组成状态集合 S。随机现象便是状态的变化过程。在某时刻 t 的状态 St 通常取决于 t 时刻之前的状态。我们将已知历史信息
- 在强化学习中,对于环境(系统)状态变化和奖励更新具有马尔可夫性质的序贯决策问题,我们需要考虑动作的影响,所以扩展为马尔可夫决策过程:下一个状态取决于当前状态和当前动作,公式为:
P(St+1∣St,At)。这是强化学习的理论基石,为什么这个概念如此重要?马尔可夫决策过程解决了三个核心问题:- 状态简化:利用马尔可夫性质,让我们只需关注当前状态而非全部历史;
- 用状态转移概率描述动作如何影响环境;
- 通过价值函数将长期奖励目标转化为可计算的数学问题。
- 马尔可夫决策过程核心元素符号化表示为五元组(S,A,P,R,γ), 其中:
- S:状态空间
- A:动作空间
- P:状态转移概率矩阵 $ P(s’ \mid s,a) $
- R:奖励函数$R(s,a,s’)$
- $\gamma $:折扣因子,为何要引入折扣因子(或称为衰减因子)。所谓折扣,就是对未来回报的价值进行折现。折扣因子的设置背后有着深刻的数学、经济学和现实考量。从数学角度看, $\gamma < 1$确保无限长轨迹的累积奖励有界收敛,避免奖励值趋向无穷大。从智能决策的角度,折扣因子还能避免”无限延迟奖励”的悖论。想象一下,如果没有折扣,AI可能为了等待某个”最大奖励”而永远不采取行动,这显然不合理。$\gamma $直接影响智能体的”远见程度”,当折扣因子越接近于 1 越关注未来收益,越接近于 0 越关注当前收益。
关键符号的延伸说明:
- 状态与转移概率:用 $P(s’\mid s,a)$ 表示,指在状态 $ s $ 执行动作 $ a $ 后转移到状态 $ s’ $ 的概率,即:$ P(s’\mid s,a) = \mathbb{P}[S_{t+1} = s’ \mid S_t = s, A_t = a] $。
- 奖励与回报 (Return):指从某一时刻开始的所有奖励的累积折扣和,用 $ G_t $ 表示,折扣因子为 $ \gamma ( 0 \leq \gamma \leq 1 $)。即,$ G_t = r_{t+1} + \gamma r_{t+2} + \gamma^2 r_{t+3} + \dots = \sum_{k=0}^{\infty} \gamma^k r_{t+k+1} $。
- 价值函数 (Value Function),在强化学习中,很多奖励是延迟的(比如游戏到最后才得分),所以我们需要用价值函数来评估某个状态或动作的长期价值。反过来说,价值函数用于评估长期收益,解决延迟奖励问题。
- 状态价值函数:$ v_{\pi}(s) $ 表示在策略 $ \pi $ 下,从状态 $ s $ 出发的期望回报,即 $ v_{\pi}(s) = \mathbb{E}_{\pi}[G_t \mid S_t = s] $
- 动作价值函数:$ q_{\pi}(s,a) $ 表示在策略 $ \pi $ 下,从状态 $ s $ 执行动作 $ a $ 后的期望回报,即 $ q_{\pi}(s,a) = \mathbb{E}_{\pi}[G_t \mid S_t = s, A_t = a] $
-
最优策略:$ \pi^* $ 是使所有状态价值函数最大化的策略,满足 $ \pi^(s) = \arg\max_a q_{\pi}(s,a), \forall s \in S $。且最优状态价值函数 $ v^(s) $ 和最优动作价值函数 $ q^(s,a) $ 满足 $ v^(s) = \max_a q^(s,a) $,$ q^(s,a) = r(s,a) + \gamma \sum_{s’} P(s’ s,a) v^*(s’) $。
轨迹与MDP要素的关系:
-
轨迹由MDP的五要素自然生成:智能体根据策略 $\pi_\theta(a s)$ 选择动作,环境根据状态转移概率 $P(s_{t+1} s_t, a_t)$ 更新状态,根据奖励函数 $R(s_t, a_t)$ 给出奖励 - 轨迹的概率: \(P(\tau|\theta) = P(s_0) \prod_{t=0}^T \pi_\theta(a_t|s_t) P(s_{t+1}|s_t, a_t)\)
- 轨迹的总奖励: \(R(\tau) = \sum_{t=0}^T \gamma^t r_t\)
强化学习在数学上,就是在马尔可夫决策过程的框架下,通过蒙特卡洛采样或者时序差分的方法,利用随机梯度上升去优化一个策略函数的参数,使得该策略在概率空间中产生的轨迹能够获得最大的累积期望回报。
分类
在强化学习(Reinforcement Learning, RL)的发展历程中,研究者始终面临一个核心问题:如何设计智能体的决策机制以实现长期收益最大化?这一问题催生出两大主流研究范式——基于价值的方法(Value-based Methods)和基于策略的方法(Policy-based Methods)。
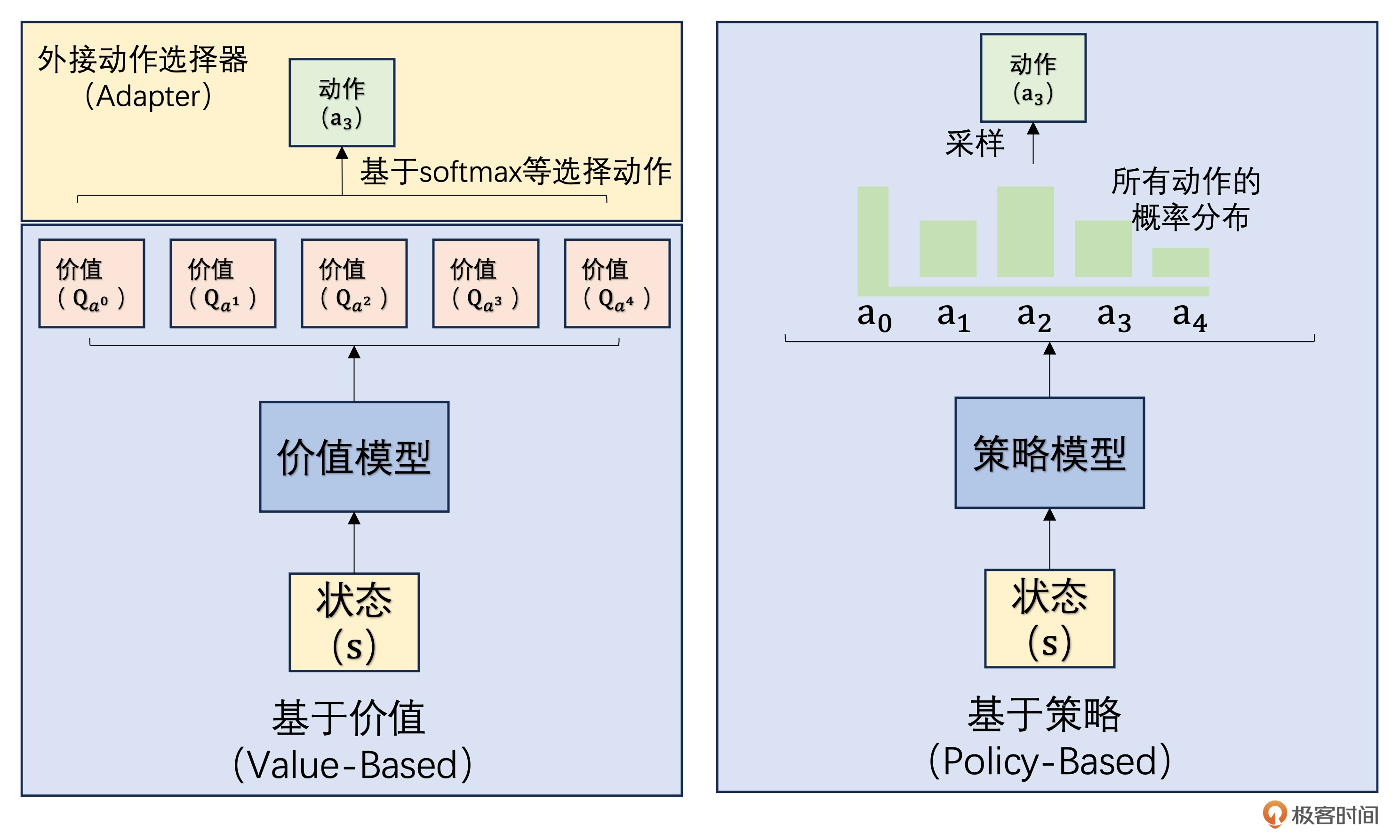
基于价值的强化学习(参考)
在强化学习中,智能体的目标是通过与环境交互最大化累积奖励。但面对复杂环境,我们需要一种工具来评估“在某个状态下采取某个动作是否划算”——这就是价值函数的作用。智能体处于某状态时,依据当前状态与可选动作,查询 Q-table,就能得到对应的 Q 值。Q-Learning 算法通过不断与环境交互(试错),更新 Q 表中的 Q 值,让智能体逐渐学到:在什么状态下,执行什么动作,能获得更高的长期收益,最终掌握最优决策策略(比如游戏通关、机器人高效导航)。
- Q-table(Q 表):是存储“状态 - 动作 - Q 值”对应关系的数据结构,可理解为一张表格,行代表环境的不同状态(State),列代表智能体可执行的动作(Action),单元格数值就是 Q 值(Q-value)。
- 状态(State):智能体所处的环境快照,比如游戏里的当前关卡、角色位置;机器人导航中的坐标、障碍物分布等,是决策的环境基础。
- 动作(Action):智能体在当前状态下可选择的操作,比如游戏角色“移动、攻击、跳跃”,机器人“前进、转向、停止”等,是智能体与环境交互的手段。
- Q 值(Q-value):对“在某状态执行某动作后,未来累计收益”的估计。数值越高,代表该动作在当前状态下越“有价值”,是智能体学习“最优策略”的核心依据。
为了更精准地理解 Q 函数的作用,我们先明确强化学习中与“价值评估”相关的三个核心概念:奖励、回报与价值函数。
- 奖励(Reward):环境对智能体动作的即时反馈,用 $ R_t $ 表示。比如游戏中吃到金币得 10 分,碰到敌人扣 50 分。
- 回报(Return):从当前时刻开始的累积折扣奖励,公式为:$ G_t = R_t + \gamma \cdot R_{t+1} + \gamma^2 \cdot R_{t+2} + \dots + \gamma^{n - t} \cdot R_n $,其中 $ \gamma $ 是折扣因子($ 0 \leq \gamma \leq 1 $),用于权衡即时奖励和未来奖励的重要性。简单来说,回报是“从现在开始,所有未来奖励的加权总和”,折扣因子 $ \gamma $ 越接近 1,说明智能体越重视长远奖励;越接近 0,则更关注即时奖励。
-
动作价值函数(Q 函数):在状态 $ s $ 采取动作 $ a $ 后,遵循策略 $ \pi $ 能获得的期望回报,公式为:$ Q_{\pi}(s_t, a_t) = \mathbb{E}[U_t S_t = s_t, A_t = a_t] $,$ Q_{\pi}(s, a) $ 就是“在状态 $ s $ 做动作 $ a $ 的好坏程度”的量化指标。一旦找到 $ Q_(s, a) $,智能体在任意状态 $ s $ 下,只需选择对应 $ Q $ 值最大的动作 $ a $(即 $ a = \arg\max_a Q_(s, a) $),就是最优策略。 - 最优动作价值函数:在所有可能的策略中,能获得的最大 $ Q $ 值,公式为:$ Q_*(s_t, a_t) = \max_{\pi} Q_{\pi}(s_t, a_t), \forall s_i \in (S), a_t \in (A) $。
我们的目标就是找到这个最优 $ Q $ 函数,因为它能直接告诉我们“在任何状态下该做什么动作”。Q-table 作为 Q 函数最基础的具象化形式,通过表格结构直接存储每个(状态,动作)对对应的 Q 值,实现价值信息的直观映射。当系统的状态空间与动作空间均为离散类型且规模可控时,Q-table 凭借其简洁的结构和高效的查询能力,成为价值函数表征的理想选择。当状态和动作是连续空间时,$ Q $ 函数的输出是对每个(状态 - 动作)对的价值估计,此时无法用表格存储,需通过函数近似(如神经网络)拟合。Q - learning 使用表格的形式,对离散的动作价值函数进行表示;DQN 使用一个参数为 $ \theta $ 的神经网络来拟合 $ Q $ 函数,可以通过梯度下降来更新网络参数 $ \theta $ 的值,从而逼近真实的 $ Q $ 函数。
基于策略的强化学习(参考)
在强化学习的策略梯度方法中,“策略”是定义智能体行为逻辑的核心要素,它本质上是智能体在环境状态(State)与动作(Action)之间建立的映射规则,通常用符号 $\pi(a \mid s)$ 表示,直观理解为“当智能体处于状态 s 时,选择执行动作 a 的倾向性或概率分布”。策略梯度方法中的“策略”,标志着智能体优化目标的关键转变:它不再是被动地对环境建模(如估计状态价值),也不是通过价值判断间接选择动作,而是直接将“策略本身”作为优化对象——通过梯度上升等数学方法,持续调整 $\pi(a \mid s)$的参数,让策略生成的行为序列在与环境的互动中,最终实现“长期期望奖励”的最大化。
深度强化学习中,策略函数通常由神经网络实现,通过多层非线性变换将状态特征映射为动作分布参数。这种端到端的表示方式避免了人工特征工程,引入非线性变换,极大提升了策略的表达能力。策略优化的核心目标是找到最优参数$\theta^*$,最大化智能体在环境中的期望累积奖励。
策略梯度方法的理论基础是策略梯度定理(Policy Gradient Theorem),该定理揭示了目标函数梯度与策略参数的关系。策略梯度方法的理论基础是策略梯度定理(Policy Gradient Theorem),该定理揭示了目标函数梯度与策略参数的关系。对于任意策略参数化形式,目标函数的梯度可表示为:$ \nabla_{\theta} J(\theta) = \mathbb{E}{\pi{\theta}} \left[ \sum_{t=0}^{\infty} \nabla_{\theta} \log \pi_{\theta}(a_t \mid s_t) G_t \right] $ 。其中 $ G_t = \sum_{k=t}^{\infty} \gamma^{k-t} r_k $ 为从时刻 $ t $ 开始的累积折扣奖励(Return)。这一优雅的公式将目标函数梯度转化为可通过采样估计的期望值,为策略优化提供了可行路径。定理的推导基于马尔可夫决策过程(MDP)的特性,通过对目标函数进行全导数展开,利用策略与状态分布的链式关系,最终消去了难以计算的状态分布梯度项,仅保留可采样的轨迹项。这一关键简化使策略梯度方法具备了实际可行性。PS:策略梯度定理的详细推导涉及较多数学技巧,若你对策略梯度的推导过程非常感兴趣,想提前了解背后的原理。推荐你参考 John Schulman 大神(TRPO、GAE 和 PPO 的作者,这个星球上没有人比他更懂策略梯度)在 2017 年 Deep RL Bootcamp Lecture 上的讲座。
早期的策略梯度算法 REINFORCE(Williams, 1992)正是基于这一原理实现,其完整流程如下:
- 基于当前策略 $\pi_{\theta}$ 采样多条轨迹;
- 计算每条轨迹中每个时刻的累积回报 $G_t$;
- 估计策略梯度$ \hat{g} = \frac{1}{N} \sum_t \nabla_{\theta} \log \pi_{\theta}(a_t \mid s_t) G_t $
- 执行梯度上升更新$ \theta \leftarrow \theta + \alpha \hat{g} $
| REINFORCE(是基于蒙特卡洛采样的策略梯度方法,所谓蒙特卡洛,可以简单理解为 Agent 的采样策略是从开始状态一直到最终状态,采样一个完整的轨迹。蒙特卡洛(Monte-Carlo/MC)通常和时序差分(Temporal-difference/TD)作为对比概念,一个方差大,一个偏差大,下一节会进行更详细的介绍)算法结构简单,但存在梯度估计方差大的问题,导致收敛速度慢且不稳定。为缓解这一问题,研究者提出了基线调整(Baseline Subtraction)技术,将梯度估计修正为:$ \hat{g} = \sum_{t} \nabla_{\theta} \log \pi_{\theta}(a_t | s_t)(G_t - b(s_t)) $,其中 $ b(s_t)$为基线函数(通常用状态价值函数 $ V(s_t) $ 估计)。理论证明,基线的引入不改变梯度的无偏性,但能有效降低估计方差,显著提升算法稳定性。 |
rl的难点
强化学习的反馈通常表现为稀疏且延迟的奖励信号,这种奖励函数可以被视为一种远期的、非直接的“正确目标”。无监督学习处理的数据通常是静态且无关联的,其经典假设是数据点之间独立同分布。相比之下,强化学习处理的是典型的序列决策问题,其数据由状态、动作和奖励组成的序列在时间上高度相关,并且不满足独立同分布条件。这种时间依赖性和序列相关性是强化学习算法设计复杂性的主要来源,也是其区别于其他学习方法的核心特征。
- reward delay. 只有最后一个token$r_T$非0,中间$r_t$=0
- agent’s actions affect the subsequent data it receives.
Policy Gradient(策略梯度)
李宏毅老师对Policy Gradient的讲解,最原始的Policy Gradient 直接$A_t=G_t$

The Definitive Guide to Policy Gradients in Deep ReinforcementLearning:Theory, Algorithms and Implementations Policy Gradient 论文综述。
DeepSeek-R1: Incentivizing Reasoning Capability in LLMs via Reinforcement Learning
一些基础概念(LLM训练任务下好理解版):
- $\pi$(Policy,策略):即LLM模型
- $\theta$(Parameter,参数):即模型参数
- s(State,交互状态):即上文,初始状态即为$s_1$
- a(Action,交互行为):即输出的token,可以简单理解为每个字符。(实际上一个字不等于一个token)
- $\tau$(Trajectory,轨迹):$\tau = { s_1,a_1,r_1,s_2,a_2,r_2,…,s_T,a_T,r_T }$
Reward Function(奖励函数定义,即输出序列$\tau$ 能获得的奖励),用于评估某个状态/动作序列的好坏:
\[R(\tau) = \sum_{t=1}^{T} r_t\]因为actor输出有一定的随机性,即对与同一个$s_t$,actor不一定每次都输出$a_t$,自然each $\tau$ has a probability to be sampled(PS:采样出来的数据分布不一定是真实的数据分布). 这个probability用$p_\theta(\tau)$ 或 $p(\tau \mid \theta)$ 表示,连带$R(\tau)$也是随机的(所以不能单纯用标量,要计算期望),所以模型参数 $\theta$ 下的Expected Reward(期望奖励)表示为sum over all possible trajectory:
\[\overline{R}_\theta = \sum_{\tau} R(\tau) p_\theta(\tau)\]综上,我们希望调整模型参数 $ \theta $ 使这个期望奖励越大越好,因此可得Policy Gradient公式如下,期望做gradient ascent最大化期望奖励:
\[\nabla \overline{R}_\theta = \sum_{\tau} R(\tau) \nabla p_\theta(\tau)\]其中 $R(\tau)$ 来自environment 反馈(it can even be a black box),跟$\theta $没关系,所以做gradient的时候只对$p_\theta(\tau)$ 做gradient即可。
我们分别来看 $R(\tau)$ 和 $p_\theta(\tau)$ 可以被约等为什么样子。
从轨迹奖励到action得失
\[\nabla \overline{R}_\theta = \sum_{\tau} R(\tau) \nabla p_\theta(\tau) = \sum_{\tau} R(\tau) p_\theta(\tau) \frac {\nabla p_\theta(\tau)}{p_\theta(\tau)} = \sum_{\tau} R(\tau) p_\theta(\tau) \nabla \log p_\theta(\tau) \quad \text{\# Note: } \nabla f(x) = f(x) \nabla \log f(x)\]
直接对$p_\theta(\tau)$ 求导无法计算,$R(\tau) p_\theta(\tau)$是期望形式,可以通过采样足够多的轨迹来估计。
\[\sum_{\tau} R(\tau) p_\theta(\tau) \nabla \log p_\theta(\tau) \approx \frac{1}{N} \sum_{n=1}^{N} R(\tau^n) \nabla \log p_\theta(\tau^n) \quad \text{\# 实际上就是N个sample轨迹近似期望}\]接下来的问题是如何计算 $\nabla \log p_\theta(\tau^n)$, 其中,模型参数$\theta$ 下生成序列$\tau$ 的概率如下:
\[p(\tau \mid \theta) = p_\theta(\tau) = p(s_1) p_\theta(a_1|s_1) p(s_2|s_1, a_1) \ldots = p(s_1) \prod_{t=1}^{T} p_\theta(a_t|s_t) p(s_{t+1}|s_t, a_t)\]轨迹概率可以分解为动作条件概率的连乘,对数概率可以拆成每一步的 log 概率之和。

忽略掉跟 $\theta$ 无关的项( 环境无法作用gradient 所以可以移除)

| $\nabla p_\theta(\tau)$ 转换为 $\nabla p_\theta(a_t^n | s_t^n)$ 之后可以通过实际采样到的 (s, a) 对来计算。 |
其中(用到了对数求导),分母$p_\theta(a_t \mid s_t)$ 体现了重要性比重:小概率但被采样到的动作,对梯度更新影响会更大(因为这说明策略应该更重视它)。避免了在采样过程中采到很多奖励值很低但是出现频次高的动作,造成模型对这种低奖励值高频次动作的偏好。 整体而言,相当于用$p_{\theta}(a_t \mid s_t)$做了某种归一化。

直观理解:在某个state(上文)下执行某个action(token)使得最后整个输出$ \tau$ 的reward是正的时候,我们应该增加这个输出的几率,反之减少。each training data is weighted by $R(\tau^n). $ PS:rl就是,判断哪个输出更好,把这个输出的概率提高,花活在于提高多少。可以给action model 每个token算loss 了。进而是不是可以理解为rlhf和sft的反馈粒度都是token?
以上是REINFORCE 算法的核心更新公式,在此基础上,可以引入 baseline(不影响期望,减少方差)、优势函数(A3C, PPO 等方法),改进收敛效果。
$R(\tau)$可以被约等为什么样子
如果仔细看上述公式,首先,它并没有告诉我们轨迹中某个单独的动作到底好不好,其次会发现 $ R(\tau) $ 即reward恒为正的情况,那会导致一直在增加任何token的输出概率。我们希望调小概率时,reward应该是个负的。直观的想法,如果我见过一批reward,减去他们的均值就好了,这个方法叫REINFORCE with baseline,让reward有正有负,这对rl的训练效率至关重要。这个方法搞出来的均值baseline不一定是最好的,我们想知道的是此刻状态对应的价值,均值没有这样的物理意义,是不是可以用一个NN模型来预估出这个价值呢?这就是Actor-Critic方法。Actor就是你的动作概率模型,Critic就是用一个NN在算这个baseline,或者我们叫他value-base的model。如果不用一个model来估计状态的价值,还有什么好办法?那你就基于每一条原始样本生成一组序列,用他们的reward均值作为baseline,这种方法叫self-critic,它利用了蒙特卡洛方法代替了TD error。
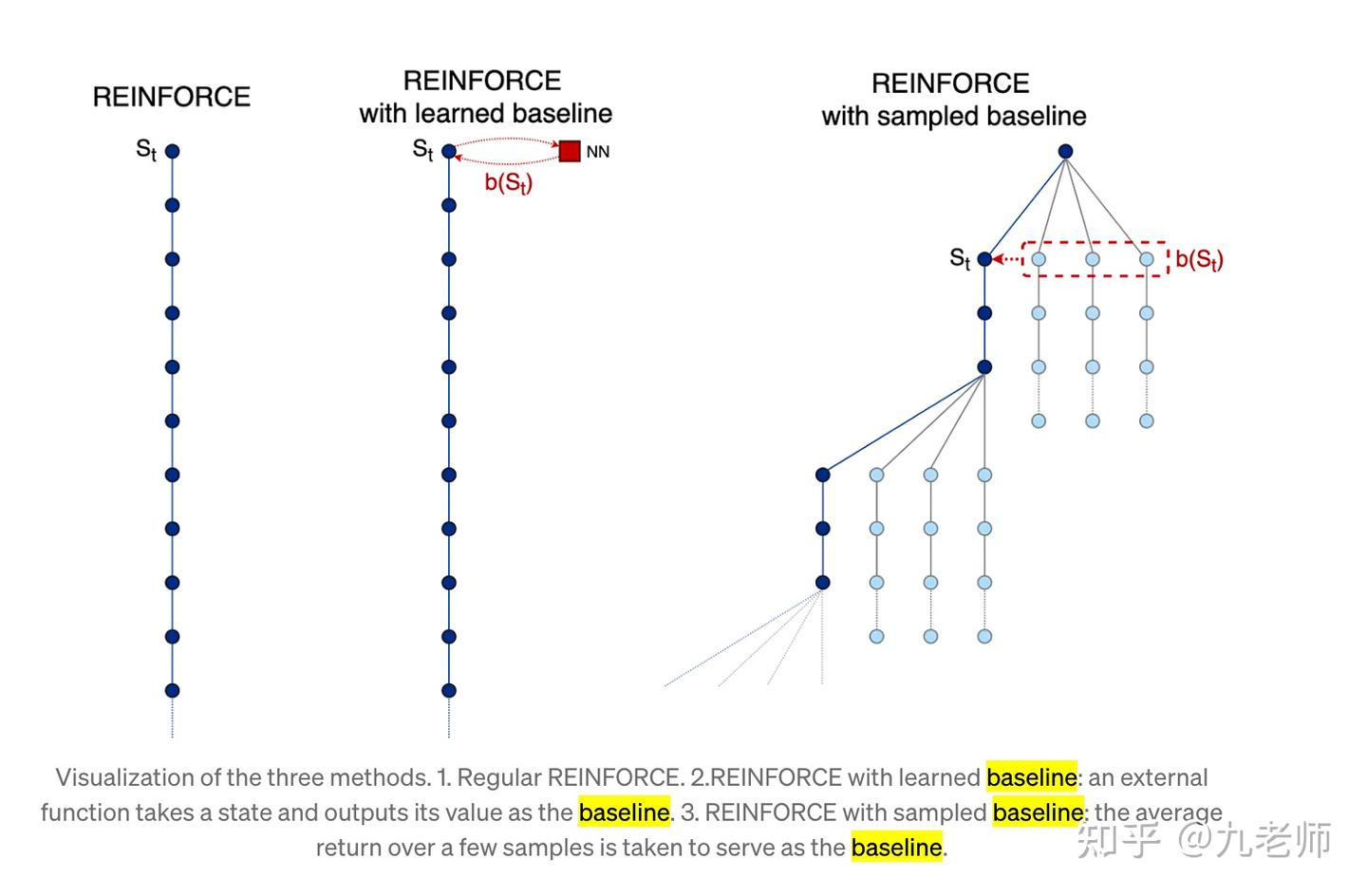
我们实际操作中是用sample的方式来训练,这就导致某些项实际上因为没被sample到(只是没被采样到,并不代表它们不好)而导致输出概率下降(实际ground truth是要提升)。所以我们希望引入一个baseline(b)让reward不是恒为正。公式变成如下:
\[\nabla \overline{R}_\theta = \frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_n} (R(\tau^n) - b) \nabla \log p_\theta(a_t^n \mid s_t^n)\]通常我们可以将baseline设置为reward的期望值,即 $ b \approx E[R(\tau)] $。
我们知道最终输出的是一个序列 $ \tau $,且在算reward时是以 $ \tau $ 的粒度计算的(episode-level reward)(PS:reward只能告诉我们哪个$ \tau $ 更好)。即使整体的reward是正的,也不意味着序列中的每一个action都是有收益的(如:说了一串废话,最后才说对结果)。因此,更合理的做法是我们需要给每一个action合适的credit(action/token-level reward)。
首先,我们会有一些假设(注意:并不一定什么情况下都适用,应根据具体情况使用不同的reward function):
-
reward应单独为每个action计算(前面的)
\[R(\tau^n) \rightarrow \sum_{t'=t}^{T_n} r_{t'}^n \quad \text{\# 计算当前action后所有reward的总和作为当前action的reward}\] -
越快完成任务应越重要,距离越远贡献越小
\[R(\tau^n) \rightarrow \sum_{t'=t}^{T_n} r_{t'}^n \rightarrow \sum_{t'=t}^{T_n} \gamma^{t'-t} r_{t'}^n \quad \text{\# } \gamma \text{为时间衰减函数}\]
实际上 $R(\tau^n) - b$ 这一项其实是在算在某个state下执行某个action比执行其他action有多好,也就是我们常说的Advantage Function,可以表示为 $A^\theta(s_t, a_t)$ ,因此综上公式可以写作:
\(\nabla \overline{R}_\theta \approx \frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_n} A^\theta(s_t, a_t) \nabla \log p_\theta(a_t^n \mid s_t^n)\) \(= E_{(s_t, a_t) \sim \pi_\theta} [A^\theta(s_t, a_t) \nabla \log p_\theta(a_t^n \mid s_t^n)]\)
前文提到 each training data is weighted by $R(\tau^n)$,从上述公式我们看到each action is weighted by $A^\theta(s_t, a_t)$. 此时所有$a_t$的一样$A_t$,都是$R(\tau^n) - b$。
在 LLM RL 中,奖励通常是一个 scalar reward( sequence-level ),然而,由于序列级似然的数值范围极大,且由此带来的梯度估计具有极高的方差,Sequence-level Objective 很难优化。LLM RL 算法通常采用 Token-level Objective。$\mathcal{J}^{\text{token}}(\theta) \approx \mathcal{J}^{\text{seq}}(\theta)$,提高 LLM RL 稳定性的方法可以理解为:如何维持这一近似的有效性。
actor-critic
PPO理论推导+代码实战 建议细读。
Actor-Critic架构为什么要有Critic呢?这就涉及强化学习的算法稳定性问题。与监督学习(SL)相比,RL实际上是很难稳定的一类训练机制。大致的原因如下:
- RL本身是处理动态系统的最优控制问题,而SL是处理一个静态优化问题。动,就比静更难处理。
- 加上RL的数据非稳态,Env-agent交互机制的数据采集量少,这使得梯度计算的方差更大,方差一大就容易偏离预期目标,算法就容易跑飞了。主流的强化学习算法是怎么解决这一问题的呢?加上Critic,使用State-value function或者Action-value function稳定策略梯度的计算过程。更高级一些的算法是采用Advantage Function,也就是加上了Baseline,增加梯度计算的稳定性。这是AC算法总是优于REINFORCE算法的原因之一。
- 如果没有Critic,PPO只能使用蒙特卡洛的完整轨迹回报(高方差)或单纯依赖即时奖励(短视),导致训练低效甚至失败。Critic的引入使得PPO能通过时序差分(TD)学习高效地估计价值,平衡偏差与方差。 PS: 配套的actor-critic 架构就得有actor model 和critic model
为何引入critic
A用 $A=G_t$, $A=G_t^{\prime}$,$A=G_t^{\prime}-b$(此处b 是一个恒定值) 这类公式直接算不太靠谱, 所以就想着用一个network 来估计baseline,即$V^\theta(s)$。它是一个Value function(也就是critic network),输入是s(注意不是(s,a)),输出是一个scalar,表示针对 actor $\theta$,the discounted cumulated reward expects to be obtained after seeing s。PS: 就好比仅看当前棋局(不是判断走下一步)就给出输赢的概率。
critic 如何用在训练actor上?将critic scalar/score作为baseline。A用 $G_t^{\prime} - V^\theta(s)$来表示。

$V^\theta(s)$ 可以认为看到s后所有动作a带来的return均值

这里有个问题,$G_t^{\prime}$ 只是s 采取动作$a_t$ 后某一个动作序列(sample)的return,可能这个sample 特别好或特别坏,所以不能充分反应$a_t$ 的好坏,因此把$G_t^{\prime}$ 换一下,用平均减平均,A用 $r_t + V^\theta(s_{t+1}) - V^\theta(s)$来表示。也就是Advantage Actor-Critic(A3C)方法。


actor 和critic都是一个network,他们输入都是一样的,都要理解s(棋谱、游戏、llm),actor 输出action,critic 输出scalar,它们network的前大半一般是一样的。
reward shaping。到目前,rl 的过程就是收集一系列<s,a,r>,对r进行整理后得到一系列<s,a,A>,之后就可以训练actor。但我们特别担心一个情况(sparse reward问题):大多数时候$r_t$都是0(人生很多时候何尝不是这样)。此时要(除了env真正的reward之外)提供一些额外的reward(如何定义reward 需要domain knowledge)。就好比孩子study原本env $r_{t+1} = -1$ 孩子不开心,你通过给他一个棒棒糖,改变了study的reward。
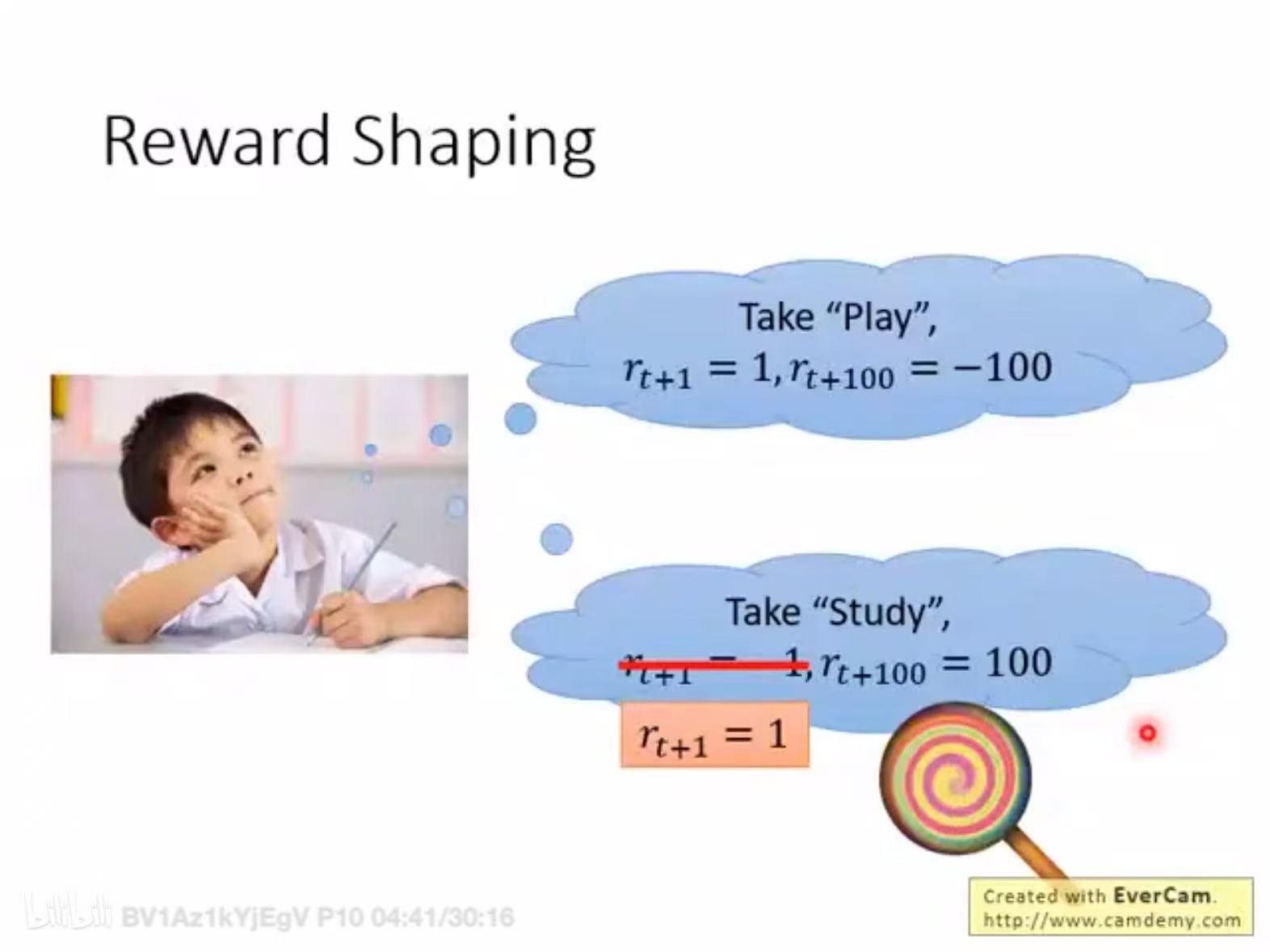
PS:此时每个$a_t$的$A_t$不同了,$A_t = R_t - V(s_t)$
GAE
TD偏差大但方差小,Monte Carlo偏差小但方差大。GAE目的是在估计优势函数时,降低方差、同时控制偏差。PS:在只有终点奖励(如 0/1)的情况下,稳定、高效地把最终奖励“分摊”到每一个 token 的决策上。在 PPO 中,真正用来更新 policy 的不是 reward,而是 Advantage。如何估计每个action的$A_t$。
在训练开始阶段, $V_{\pi}$很有可能无法刻画真实的状态价值,我们可以选择少信任$V_{\pi}$的计算结果,将 $V_{\pi}(s_{t+1})$展开得:
\[r_t + \tau V_{\pi}(s_{t+1}) - V_{\pi}(s_t) = -V_{\pi} + \sum_{l=0}^{\infty} \gamma^l r_{t+l}\]其中,$r_t,r_{t+1},r_{t+2},…$都是我们某次采样得到的即时奖励数据。如果$V_{\pi}$不准,那就信任实际采样结果,这样至少不会对优势函数的估计出现偏差。
\[A_t^{GAE} = \sum_{l=0}^{\infty} (\gamma^{\lambda})^l \delta_{t+l}\]\(\delta_{t+l} = r_t + \tau V_{\pi}(s_{t+1}) - V_{\pi}(s_t)\) 当 $\lambda$ 接近0时,$A_t^{GAE}$ 退化成一步TD误差:$r_t + \tau V_{\pi}(s_{t+1}) - V_{\pi}(s_t)$。
当 $\lambda$ 接近1时$A_t^{GAE}$ 变成 $-V_{\pi} + \sum_{l=0}^{\infty} \gamma^l r_{t+l}$ GAE 使用整个剩余奖励序列来估计优势。记这种引入了GAE方法的单步优势为 $A_t^{GAE}(s_t,a_t)$,新的策略梯度调整为:
\(\nabla J(\pi_{\theta}) = \underset{\tau \sim \pi_{\theta_{old}}}{E_t} \left[ \frac{\pi_{\theta}(a_t | s_t)}{\pi_{old}(a_t | s_t)} A_{\pi}^{GAE}(s_t, a_t) \nabla log \pi_{\theta}(a_t | s_t) \right]\) 由于 $\nabla f(x) = f(x) \nabla log f(x)$,上式可以改写为: \(\nabla J(\pi_{\theta}) = \underset{\tau \sim \pi_{\theta_{old}}}{E_t} \left[ \frac{\nabla \pi_{\theta}(a_t | s_t)}{\pi_{old}(a_t | s_t)} A_{\pi}^{GAE}(s_t, a_t) \right]\) 我们的优化目标变成: \(\arg\max_{\pi_{\theta}} J(\pi_{\theta}) = \underset{\tau \sim \pi_{\theta_{old}}}{E_t} \left[ \frac{\pi_{\theta}(a_t | s_t)}{\pi_{\theta old}(a_t | s_t)} A_{\pi}^{GAE}(s_t, a_t) \right]\)
如何学习critic/critic_loss 演化过程
critic模型可以提供可靠的token级别的中间价值估计(critic用来计算$v(s_t)$的,作为一个baseline),在RLHF场景,因为PRM比较难,那么存在下面的计算reward的方式:
- 对于t如果是中间token,那么其通常r=0(或者为了防止模型崩坏加的微小 KL 散度惩罚)。
- 对于t是结尾的token,那么其通常等于奖励模型打出的得分。
critic模型的另外一个作用是:可以将最后的 Reward 分配到中间步骤(Token-level)。他是如何做到的呢?假设已经有了一个训练好的critic模型,它可以判断当前已经生成的句子的好坏程度。对于中间token的优势,上文提到我们有GAE来计算:假设简略版本的GAE是这 \(A_t \approx r_t + \gamma V_{\pi}(s_{t+1}) - V_{\pi}(s_t)\)
由于中间token的奖励是0(或者微小的负的kl散度),$\gamma =1$,$0 < \lambda < 1$。那么
\[A_t \approx V_{\pi}(s_{t+1}) - V_{\pi}(s_t)\]因此一个好的critic模型可以:可以将最后的 Reward 分配到中间步骤(Token-level)
说如何计算/训练$V^\theta(s)$?
- Monte-Carlo(MC) based approach。 $V^\theta(s)$ 与 $G_t^{\prime}$ 越接近越好。约束是你得拿到完整的episode(比如你得玩完整场游戏)。

- Temporal-difference(TD) approach。$V^{\theta}(s_t) - \gamma V^{\theta}(s_{t+1}) $与$r_t$越接近越好。适合无法拿到完整的episode的场景。

PPO理论推导+代码实战 不如这里详细。
关于critic_loss 第一想法是: $critic_loss =(R_t + \gamma * V_{t+1} - V_{t})^2 $
最小化TD Error(TD误差就是预测误差:实际观察到的和预测的差距)就可以训练一个预测状态价值的Critic model,critic优化是:
\[\arg \min_{V_{\pi}} L(V_{\pi}) = E_t[(r_t + \gamma V_{\pi}(s_{t+1} - V_{\pi}(s_t))^2)]\]Reward Model提供环境的基础反馈信号(即$r_t$),是Critic学习的输入。Critic Model将即时奖励转化为长期价值估计,指导策略优化方向。
- 只有Reward Model:只能提供即时奖励信号(如生成完整句子后的总分数),但无法评估每个 token 或部分响应的长期价值,使策略更倾向于选择长期回报更高的动作。
- 只有Critic Model:若奖励函数未知(如逆强化学习),Critic无法凭空学习价值函数。 在PPO中,Reward Model提供基础的真实反馈,而Critic Model将其转化为长期价值估计,两者缺一不可。
总结一下
所有RL算法都是在解决策略梯度存在的两个问题
- 绝对优势问题(没有减去baseline导致方差大) 。不同轨迹的 $R(\tau_i)$ 是不同的,而且我们是采样了一些轨迹,如果我们采样的轨迹 $R(\tau_i)$ 都是正的,把轨迹中对应的动作都提高,但一些我们没有采样到,是正确答案的轨迹对应的动作就得降低,因为,我们不希望奖励总是正的,而是要减去一个基线(平均回报),表示相对优势。只有一个动作相比相对优势是正的,我们才提高其动作的概率,如果相比相对优势是负向的,我们要降低其动作的概率。
- 价值评估函数 ==> 入状态价值函数和动作价值函数 ==> 优势价值函数=动作价值函数-状态价值函数
- 绝对优势 ==> 引入baseline, baseline实现很多,PPO(value模型),GRPO(组内平均值),REINFORCE++(batch内平均值)
- 信用分配问题 (Credit Assignment Problem)。信用分配粒度过粗(细粒度的reward分配)。一个轨迹(序列)的整体的回报很高,不能说明他的每一个动作都好,我们对轨迹中所有的动作都使用相同的回报是否合理?我们希望对一个动作能有两种方法衡量其价值:1)评估动作当下的影响(单步回报);2)又能体现动作对后续策略轨迹的长远效益。(轨迹整体回报)
- 有两种典型的方法:蒙特卡洛法(MC)和时序差分法( TD) 1. Monte Carlo 方法采用最直观的评价方式:一句话最终好 → 这句话里所有 token 都好;一句话最终坏 → 所有 token 都坏,如果整句话得了 +10 分,那每个 token 都应该更常出现;如果得了 -10 分,每个 token 都应该更少出现。每个 token 获得相同的梯度信号,无法区分贡献度。 2. TD 引入一个新角色:Value Function(价值函数)V(s),也叫 Critic(评论家),它是一个预测未来 reward 的模型(通常是另一个神经网络)。它的定义是:V(s) = “从当前上下文 s 开始,我预计这句话最终能拿多少分?”
以最简单的 TD(0)(TD是一个算法家族名) 为例,最简单的 TD(0) 算法定义 TD 误差 (TD Error): \(\delta_t = r_t + \gamma V(s_{t+1}) - V(s_t)\)
其中:
- $V(s_t)$:生成这个 token 之前,我预计未来能得多少分
- $r_t$:生成这个 token 立即获得的奖励(LLM 场景下通常为 0)
- $\gamma V(s_{t+1})$:生成这个 token 之后,我现在预计未来能得多少分($\gamma$ 是折扣因子,通常接近 1)
- $\delta_t$:实际 vs 预期的差距
TD的关键点在于:每个 token 的责任被局部化了,每个 token 不再为整句话的最终命运负责,只为”我这一步有没有让情况变好”负责。
- TD 没有用最终 reward!
- TD 没用整条轨迹!
- 而是只用了当前估计和下一步估计
- 让误差被”局部化”在一步之内
但是需要注意的是,TD 不能直接用于策略更新!TD 误差 $\delta_t$ 是用来训练 Critic(价值函数)的:$V(s_t) \leftarrow V(s_t) + \alpha \cdot \delta_t$,但我们真正要做的是更新策略(Policy)——改变 LLM 生成每个 token 的概率分布。我们还需要把 TD 思想转化为策略梯度信号。这就是 Advantage 的作用:把TD 思想用在策略更新上。Advantage 不是问”这个状态有多好”(Value),而是问:”在这个状态下,选择这个 token 比平均水平好多少?”
\[A(s_t, a_t) = Q(s_t, a_t) - V(s_t) = "选这个token的价值" - "这个状态的平均价值"\]- $Q(s_t, a_t)$:在状态 $s_t$ 下选择 token $a_t$ 之后的期望总奖励(Action-Value Function)
- $V(s_t)$:在状态 $s_t$ 下,不管选什么 token,平均能得到的期望奖励(State-Value Function)
Advantage 的意义:
- A > 0:这个选择比平均水平好 → 增加概率
- A < 0:这个选择比平均水平差 → 降低概率
- A ≈ 0:这个选择就是平均水平 → 不需要调整
梯度演进
-
REINFORCE 的梯度:$\nabla \log \pi(a_t s_t) \times G_t$ -
当我们把它写成更通用的形式,可以用任何”优势估计”来替代 $G_t$:$\nabla \log \pi(a_t s_t) \times A_t$ - 在 Monte Carlo / REINFORCE 中:$A_t = G_t - V(s_t) = \text{(实际获得的总奖励)} - \text{(之前预期的总奖励)}$
- 在 TD-based 算法中:$A_t = \delta_t = r_t + \gamma V(s_{t+1}) - V(s_t)$
-
有了 Advantage,策略梯度更新变成:$\nabla \log \pi(a_t s_t) \times A(s_t,a_t)$
online/offline policy
在强化学习中,策略可以根据它们与数据生成策略的关系被分类为 on-policy 或 off-policy。这两种方法在处理经验数据和更新策略时有所不同,
- On-policy 方法直接从目标策略(即当前学习和评估的策略)中采样数据,它要求学习算法和行为策略是一致的,即生成数据的策略必须是当前优化的策略。比如用当前模型对一批问题生成回答,然后根据这些回答的质量(奖励)来调整模型参数,让它下次说得更好。这里的数据和模型是 “同步” 的 —— 数据来自 “现在的模型”,优化的也是 “现在的模型”。the agent learned and the agent interacting with the environment is the same.PS: 就好比帅哥追美女的某些招式/经验对普男反而有害。
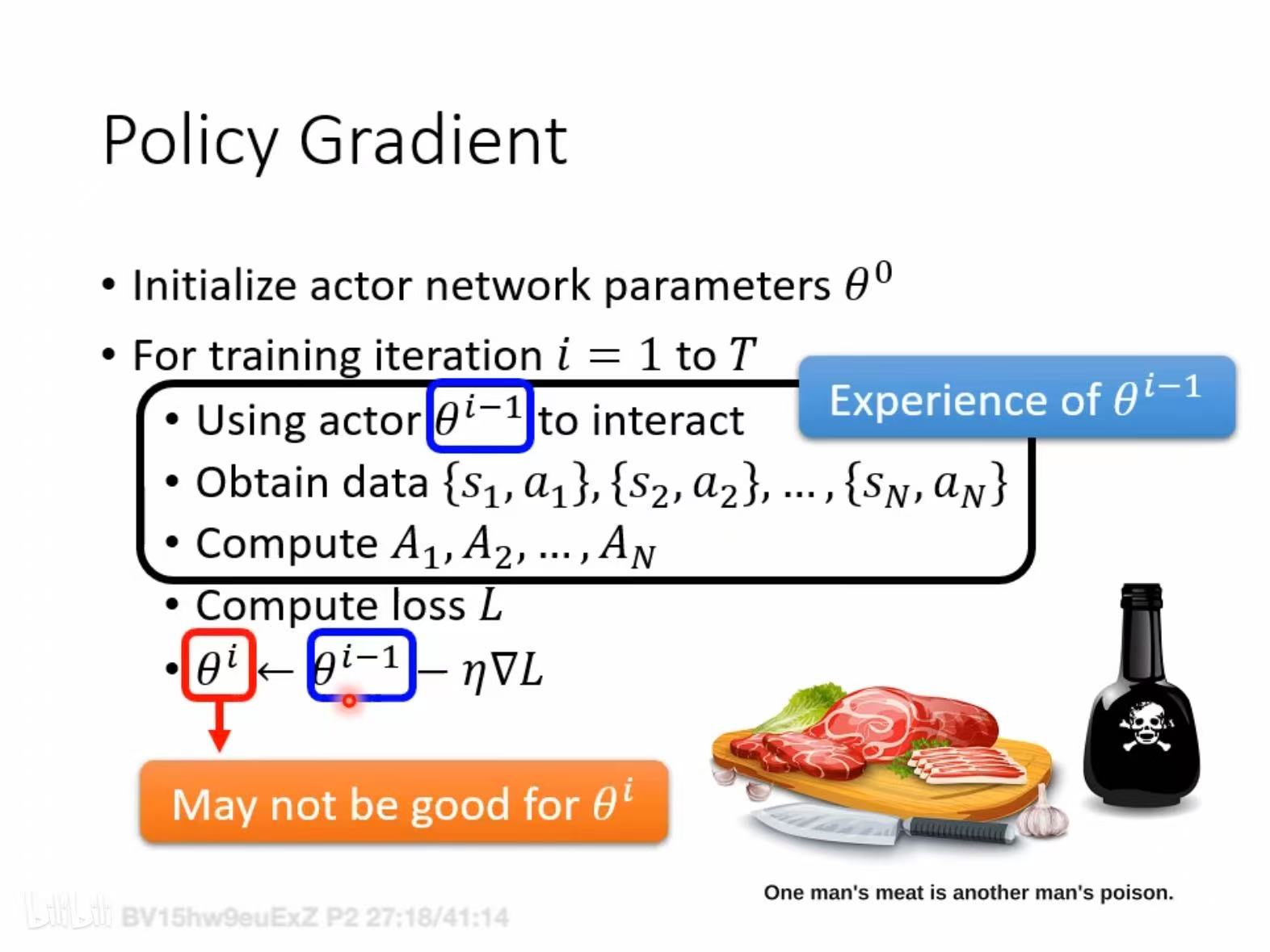 也就是在传统supervisor learning中,training data都是事先准备好的,无论跑多少次Epoch 都是一批training data,而对与rl 来说,参数要更新多少次,training data 就要更新多少次,用本轮的$\theta$ 输出的
也就是在传统supervisor learning中,training data都是事先准备好的,无论跑多少次Epoch 都是一批training data,而对与rl 来说,参数要更新多少次,training data 就要更新多少次,用本轮的$\theta$ 输出的<s,a>计算<s,a,A>来更新$\theta$,体现在代码上就是training data产生在for循环之内,也是为何rl比较耗时的原因。 - Off-policy 方法允许从与目标策略不同的行为策略中采样数据。比如训练时用的数据不是当前模型生成的,而是来自 “别人”(比如人类专家写的回答、更强的模型生成的回答,或者过去版本的模型留下的回答)。虽然这些回答不是当前模型自己说的,但可以帮它更快学到正确的模式。the agent learned and the agent interacting with the environment is different.
PS:on-policy好比自己走万里路,自己从自己的经验中学习。off-policy 类似于从别人的经验中学习。
on-policy 和 off-policy 的区别,主要体现在对数据的使用上,off-policy 的训练效率会明显更高一些。一方面,off-policy 可以不等所有的 response 生成完毕,就启动模型训练;另一方面,off-policy 可以多次使用同一条数据,提高数据利用率,on-policy 则不可以。 off-policy 的模型快速熵坍缩( on-policy缓慢熵坍缩)。防止熵坍缩:加入熵 loss 和 clip higher 。
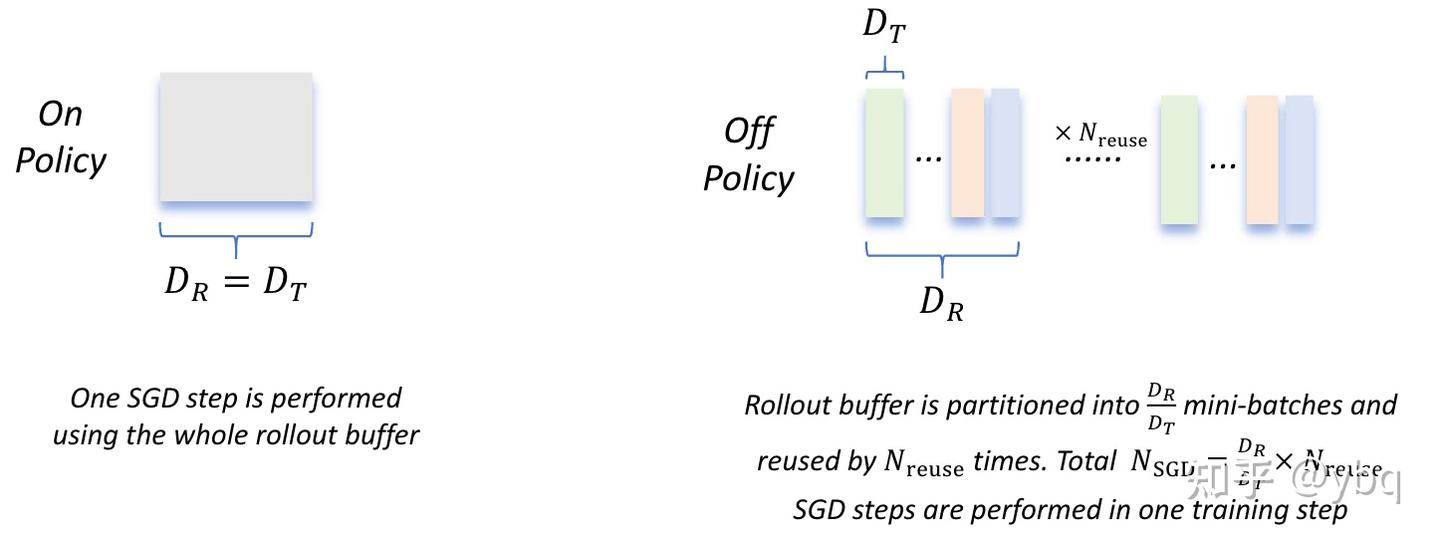
PPO叫Proximal Policy Optimization,就是揉和了online/offline policy。actor to train has to know its different from the actor to interact(产生training data的actor).
Exploration,采集trainning data时可以给actor 加一些随机性,不必每次都是s1 => actor ==> a1。

重要性采样
先不说rl,前文提高,我们可以通过足够的采样的均值来近似一个分布的期望。 \(E_{x \sim p}[ f(x)] \approx \frac{1}{N} \sum_{i=1}^{N} f(x^i)\)
当我们有两个分布$p(x)$和$q(x)$,但是又无法直接从 $p(x)$采样,但可以从$q(x)$采样时,我们可以这么描述$x \sim p(x)$下 的期望:
\[E_{x \sim p}[f(x)] = \int f(x)p(x) dx = \int f(x) \frac{p(x)}{q(x)} q(x) dx = E_{x \sim q}[\frac{p(x)}{q(x)} f(x)]\]注意从 $E_{x \sim p}$ 换成了 $ E_{x \sim q}$,通过一个 权重修正,把在 q(x) 下采样的数据“重加权”为好像来自 p(x) 的数据。其中 $w(x) = \frac{p(x)}{q(x)}$ 就叫重要性权重(importance weight),表示在 q(x) 下采样到的数据,并不都“同等重要”地代表目标分布 p(x)。重要性权重 w(x) 调整了哪些样本更“重要”。如果某个样本在目标分布 p(x) 里比在行为分布 q(x) 更可能出现(即 p/q > 1),那它就被赋予更高的权重;反,如果 p/q < 1,它就被减弱。这个过程就叫 Importance Sampling( IS,按重要性来采样/加权)。
套一下上面的公式
\[\nabla \overline{R}_\theta = E_ [ R(\tau) \nabla \log p_\theta(\tau)] = E_{\tau \sim p_{\theta'}(\tau)} [\frac{p_{\theta}(\tau)}{p_{\theta'}(\tau)} R(\tau) \nabla \log p_\theta(\tau)]\]具体到action 粒度

在实践中,我们为了降低采样成本,提升训练效率(采样是训练所需的,主要是不想对新的策略采样到的轨迹再计算奖励和优势),我们希望对得到的一批“经验”进行多次训练,过程如下:
- 假设某次更新完毕后,我们得到策略 $\pi_{old}$
- 我们用$\pi_{old}$和环境交互,得到一批经验数据(主要是状态价值、优势、回报)。
- 我们将把这一批回合数据重复使用k次:即我们先把这批数据喂给 $\pi_{old}$,更新得到$\pi_{\theta_0}$,我们再把同一批数据喂给$\pi_{\theta_0}$,更新得到$\pi_{\theta_1}$;以此类推,做k次更新后,我们得到$\pi_{\theta}$。
- 我们管这个过程叫off-policy(产出数据的策略和用这批数据做更新的策略不是同一个)。
- 在这k次更新后,我们令$\pi_{old} = \pi_{\theta}$。重复上面的过程,直到达到设定的停止条件为止。
但是在我们训练的过程中,由于策略已经发生了改变,采样出来的分布已经变了据此我们应该将新的策略梯度调整为:
\[\nabla J(\pi_{\theta}) = \underset{\tau \sim \pi_{\theta_{old}}}{E_t} [ \frac{\pi_{\theta}(a_t | s_t)}{\pi_{old}(a_t | s_t)} A_{\pi}(s_t, a_t) \nabla log \pi_{\theta}(a_t | s_t) ]\]注意,重要性采样有效的前提是p(x)和q(x)分布不能差别太大,这也是为何PPO进入KL和clip的原因。
重要性采样的目标是:为了更充分的利用rollout的轨迹,比如旧策略模型采样出来的轨迹,我们更新多次,但是这样两种期望差异比较大,因此我们引入重要性采样(具体方法不多赘述)来解决这个问题。
缺点
rl最大的缺点:效率极低。模型往往要把整个任务完整跑一遍,等到最后才知道自己做得对不对。只有在这一次尝试彻底结束后,它才能收到一个简单的结果信号。想象一下,一个系统花了几十步、上百步去写代码、下棋或解题,最后得到的只是一个模糊的提示:成功还是失败。它不知道哪一步做得好,也不清楚哪一步出错,只能靠反复试验去猜。往往要重复上千次,才能从偶然的成功里提炼出一点有价值的经验。低效的根源在于,它几乎只看结果。模型在完成一项复杂任务时,无论中间经历了多少误判和偶然,只要最后成功,就会被判定为正确。它学到的不是理解,而是取巧。强化学习让模型更会迎合奖励,却未必更聪明。现实世界的目标是模糊的、多维度的,根本无法被单一的奖励函数概括。Karpathy 更看重的,是让模型在每一步中学会理解。不是完成任务后才得到结果,而是在过程中就能意识到自己哪里做得好、哪里需要调整。这需要更细致的过程监督与反思机制,让模型能像人一样边做边学。人类的智慧并非来自被奖励,而是来自对错误的体察与对过程的理解。
其它
RL 本质是最大化“轨迹奖励 × 轨迹概率”,通过 log-trick,把问题拆到 action 粒度;Advantage/Critic/GAE/GRPO 等方法,就是在不断改进 action 粒度奖励的估计方式,让训练更稳定、更高效。
强化学习就是在与环境的交互中获得反馈,不断更新模型,最大化整个过程的累积奖励(的期望,关于轨迹的回报的期望,期望一定是关于概率分布的)。但是具体到底怎样让智能体选择合适的动作来最大化期望奖励呢,根据对环境的了解情况,可以分成两个部分:Model-based 以及 Model-free.
- Model-based:环境是一个白盒(每种状态对应的反馈已知、转移概率已知,等等),可以基于此设置策略。行为因此也受限于对环境的认知。Model-based 一族有 Value iteration, Policy iteration 等算法。
- Model-free:环境是一个黑盒,只能通过环境基于的反馈进行学习。大多数常用的 RL 算法,譬如说 Q-learning, Policy gradient,都属于 Model-free。
Model-free 具体分为
- 其中 Value-based 方法不需要一个具体的策略,而是让状态$V_{\pi}(s)$ -动作值函数 $Q_{\pi}(s,a)$ 充当隐式地承担起制定策略的角色,而不是直接优化策略。找到一个最优的价值函数,可以得到一个最优策略(只要衡量出每个动作的价值大小,自然可以采取策略)。PS:value-based 也可以用来筛选训练数据。
- $V_{\pi}(s) = E_{\pi}[G_t \mid S_t =s]$
- $Q_{\pi}(s,a) = E_{\pi}[G_t \mid S_t =s, A_t = a]$
- 优点,学习过程通常更稳定。收敛速度较快,通过贪婪策略可以间接得到最优策略。
- 缺点,只能处理离散且有限的动作空间,并且可能只能找到局部最优解。
- 而 policy-based 方法有一个显式的策略,直接对策略$\pi(a \mid s)$进行建模和优化,这是在给定状态$s$下选择动作$a$的概率分布。让策略和环境交互多次,采样足够多的轨迹数据,来评估策略的价值,再据此决定策略的迭代方向。通过直接训练策略来找到最优策略。策略通常由参数化函数表示,如神经网络$\pi_{\theta}(a \mid s)$,其中$\theta$ 是需要学习的参数,通过最大化预期累积奖励$G_t$,对$\theta$进行优化。
- 优点,能够学习随机策略;适用于高维或连续的动作空间;通常能找到全局最优解。
- 缺点,通常收敛速度较慢,且评估策略的效果(如通过蒙特卡洛方法)可能具有高方差,导致学习过程不稳定。
- actor-critic(比如PPO)是策略梯度方法与价值方法的创造性融合。
- actor 代表策略部分,负责生成动作。actor直接建模策略$\pi(a \mid s)$,并根据 Critic 的反馈调整策略参数,以优化长期奖励。
- critic,代表价值部分,负责评估采取的动作。actor根据 Critic 的反馈调整策略参数,以优化长期奖励。
没有强化学习基础也能看懂的PPO & GRPO 建议细读。
- 只有Reward时的朴素做法:为什么会有问题?奖励信号波动很大,PS:激励一直为正
- 引入 Critic,引入价值函数当参考线(baseline),从“只用 Reward” 进化成“用 Advantage 来衡量进步”
- 加入 Clip 与 min 操作:防止更新过度。比如 $\frac{P(A_t \mid S_t)}{P_{old}(A_t \mid S_t)}$ 设置一个范围,例如(0.8 ,1.2),也就是如果这个值一旦超过1.2,那就统一变成1.2;一旦小于0.8,那就统一变成0.8。相当于在超过约束范围时,我们停止对Actor模型进行更新。
- Reference Model:防止作弊、极端策略,新的行为不能和这个初始策略差太远,否则就要受到 KL惩罚。Actor 不会为了短期 Reward 而脱离原本合理的策略范畴,保证策略在演化过程中不至于“作弊”或偏得太离谱。
- PS:题外话,有文章提到KL_loss 初期基本没影响,训得久了之后(750 step 往后)就让模型训不动了。KL_loss 一直以来被诟病的就是“reference_model 为什么不定期更新一下”。都过了几千、几万step 了,还要被原始的模型来约束,非常不合理,现在很多强化工作确实也都选择不用 KL_loss 了。
- Critic(价值函数)通常需要跟 Actor 同等大小的网络去估计,否则很难评估到位,成本很高,而且有些场景(比如只在回答末尾才有一个整体 Reward)并不太适合训练出精细的价值函数。用同一问题的多条输出做平均,得到一个“相对评分”,再做标准化后作为 Advantage。
