简介
深度学习框架最重要的是什么?答:是自动求导系统。为什么要自动求导系统?答:因为目前的损失函数的优化方法全都基于一阶梯度信息进行梯度下降。如何实现梯度的计算?答:计算图。因此,pytorch 的 tensor 和 numpy 的 np.ndarray 最大的区别在于当你使用 tensor 进行加减乘除运算时,torch 后台会自动帮你构建出计算图,当你计算完成后,通过运算结果的 backward 函数反向传播后,你就可以得到一路上所有 requires_grad=True 的 tensor 的梯度了(必须是叶子节点)。因为这个过程中,每个 tensor 是计算图上的一个节点,在 HPC 或者 infra 工程师的语境中,我们更喜欢用 node 而非 tensor 来描述参与运算的单元。
手把手教你如何自己设计实现一个深度学习框架(附代码实现) 对机器学习在工程上的实现和抽象说的比较透。tinynn 只是一个「玩具」版本的深度学习框架,一个成熟的深度学习框架至少还需要:支持自动求导、高运算效率(静态语言加速、支持 GPU 加速)、提供丰富的算法实现、提供易用的接口和详细的文档等等。
发展脉络
发展脉络
大模型时代,AI框架的机遇和挑战AI框架经历了四个阶段的发展:
- 早期主要用于研究比如Theano;
- 随着CV的兴起,为了追求极致的性能加速,发展出了基于静态图的AI框架比如TensorFlow,它大大提升了性能和部署效率;
- 伴随着NLP技术的快速发展,算法复杂度大幅提升,动态图成了提升易用性的关键,典型的比如PyTorch,它有效提升了编程体验,能够与Python生态更好地融合。
- 大模型有两个比较大的特点:
- 模型结构收敛到Transformer,而且大部分是decoder only的架构;
- 模型的规模大,达到百亿/千亿级别,训练推理成本高,训练时间长。
所谓的“模型”本质上是两个部分的合体:计算图和模型参数——神经网络的本质是一个数学定义下的函数,它自身不是一个可执行的程序。举个简单的例子,假设某个模型的函数实际上就是一个二次函数$f(x)=x^2+2x+1$,那它的“计算图”就是$ax^2+bx+c$(简写,实际要变成图结构),参数就是一个字典:{a:1,b:2,c:1}。所以pytorch保存的模型文件实际上是一个python字典(key是模型层的名称,value是对应参数),你用pytorch载入一个保存好的模型,需要先在代码里import 模型定义,然后再load_state_dict。换句话说,实际发布的“模型”本身需要依附于框架而存在,不是一个可执行文件。
基本思想
纯Python实现原理级深度学习框架(一)计算图的原理,节点类的实现和计算图的可视化神经网络的几种表示
- 神经网络的拓扑结构,拓扑图结构中,不展示具体程序中变量的数据结构,只展示网络中输入数据维度的变化。这样做可以很直观的展示出张量在不同的模式空间中的变化情况。
- 还有一种更加简单的表示方式——直接用流程图。PS:比如介绍transformer那张图。
- 计算图。目前绝大多数深度学习框架都是通过计算图来实现的。以tensorflow为例,其计算图的图节点共分为三种:Placeholder,Variable和Operation。而拓扑图中张量从不同模式空间内的变换都可以转化为计算图上节点与节点直接的连线,类似数据结构课上通过构建符号树来完成一条数学表达式计算的情形。事实上,许多的商业级数学软件内部都是通过建立一颗语法树来完成对一条数学表达式的诸多操作,而神经网络内部本来就是输入数据经过一条条数学公式的变换。但是由于树不能存在环,而神经网络中的一个中间变量可能会被利用多次,而最终的输出只有一个,因此,神经网络的树结构可能存在环,因此,我们选择用图来表示神经网络是合情合理的。
节点/数据抽象
所有的节点分为数据和操作是可以理解的,但是为什么数据还要分为Variable和Placeholder呢?在神经网络中,有两部分数据是不会变的,它们是输入和标签,这两部分数据实际上是和网络独立的,只有那些网络参数会永远存在于网络中,而外部的数据随着使用的数据集的变化而变化。所以我们将那些外部输入的数据存储在Placeholder中,其余的网络参数存储在Variable中。作为网络参数,Variable在反向传播中会被更新,而输入的Placeholder虽然也会有梯度,但是Placeholder存储的是外部数据,当然不需要更新。所以有一个废话向的话语:前向运算中只有Operation中的数据需要更新,反向传播后的参数更新中只有Variable中的数据需要更新。因此三种节点的职能为:
- Placeholder: 存储外部输入数据,不参与任何的数据更新。
- Variable: 存储内部网络参数,参与反向传播后的参数更新。
- Operation: 存储该节点的运算符信息和此运算得到的运算结果,参数网络前向运算的数据更新。程序中,Operation类会派生出具体的算子类。
在具体程序中,以上的三种节点我们会写成三个类,为了更好的代码结构(其实是为了少写几行代码),这三个节点都是计算图中的节点,所以它们会具有一些相同的属性和方法。因此我们会用一个Node基类来派生出这三类节点。同样,具体的算子类和Operation类也存在继承关系。
我们先完成Node基类。考虑到每个节点都存有数据,而且我们更加习惯使用+-*/来直接操作变量,所以我们需要重载Node的一些运算符。
class Node(object):
def __init__(self):
"""
base for all types of node in the static calculation graph
"""
self.next_nodes = [] # self.next_nodes中存储了该节点的所有后继节点
self.data = None # 代表该节点存储的数据,在第一次前向运算之前,所有的节点的data都是None。
_default_graph.append(self) # 保存计算图上的所有node
def __neg__(self): # python 魔术方法,自定义运算符的行为
return negative(self)
def __add__(self, node : Node):
return add(self, node)
def __mul__(self, node : Node):
return multiply(self, node) # 乘法运算改为 multiply.__init__ + multiply.compute
...
class multiply(Operation):
def __init__(self, x : Node, y : Node, node_name: str=""):
super().__init__(input_nodes=[x, y], node_name=node_name)
def compute(self, x_v : np.ndarray, y_v : np.ndarray):
return x_v * y_v
我们希望节点创建完后就自动完成了计算图的创建,因此我们需要在每个节点创建完后为其next_nodes添加元素。但是这样不怎么好写,毕竟你又不知道创建完这个节点后,后面会有什么节点。而且能够起到连接作用的只有Operation,因为计算图中的连线可以理解为数据往函数送的过程,因此只要有连线,连线的右侧一定是Operation。因此,只要把握住每个Operation节点的前后,就可以完整地描述这一整张计算图。说得具体点吧,我们只需要为Operation节点添加一个成员input_nodes,并且在创建Operation节点时,将传入的Node填入input_nodes中,并在这个时候更新那些传入的Node的next_nodes就Ok了。
class Operation(Node):
def __init__(self, input_nodes : List[Node] = []):
super().__init__()
self.input_nodes = input_nodes
for node in input_nodes:
node.next_nodes.append(self)
def compute(self, *args): # compute方法是所有具体的算子类必须实现的方法
pass
class Placeholder(Node):
def __init__(self):
super().__init__()
class Variable(Node):
def __init__(self, init_value : Union[np.ndarray, list] = None):
super().__init__()
self.data = init_value
这样一来,当我们创建节点后,计算图就自动生成了,你可以从通过最后一个节点(一定是Operation)的input_node往前BFS或DFS得到图中的所有点,或者直接打印_default_graph就可以得到计算图的拓扑排序。至此,我们简单框架的所有的节点类就全部创建完成了,我们不妨通过简单的创建来检查一下计算图的构建是否正常,假设你现在要做波士顿房价预测,那么假如只是搭建一个单层感知机,那么会这么写:
if __name__ == "__main__":
X = Placeholder()
W = Variable(np.random.randn(13, 1))
b = Variable(np.random.randn(1, 1))
out = X @ W + b
from pprint import pprint
pprint(_default_graph)
组件/层抽象
不过许多的深度学习框架不会像这样给你提供创建矩阵变量的API,将MLP化成“表面上”的矩阵出来做矩阵乘法。它们大部分是提供一个API,告诉你调用这个API会得到一个线性层,而且这玩意儿能当函数用,比如keras的Dense,pytorch的Linear,paddlepaddle的fc(2.0版本之前,2.X的paddlepaddle的线性层创建API也改名为Linear了)。
def Linear(input_dim : int, output_dim : int, bias : bool = True):
W = Variable(np.random.randn(input_dim, output_dim))
if bias:
b = Variable(np.random.randn(1, output_dim))
return lambda X : X @ W + b
else:
return lambda X : X @ W
if __name__ == "__main__":
X = Placeholder()
out = Linear(13, 1, bias=True)(X)
from pprint import pprint
pprint(_default_graph)
常用深度学习框架提供的Linear算子中,有时可以通过”act”参数让线性层的值激活输出,而act参数是str对象,所以怎么通过一个字符串得到对应的激活函数类(Operation的派生类)呢?此处我们可以使用python的装饰器来实现激活函数类的注册,通过注册字典,我们就可以通过字符串映射到对应的激活函数类了
_register_act_functions = Register()
# 在已经实现的激活函数的上面使用装饰器装饰,装饰函数参数填对应的激活函数的名字
@_register_act_functions("sigmoid")
class sigmoid(Operation):
def __init__(self, x : Node):
super().__init__(input_nodes=[x])
def compute(self, x_v : np.ndarray):
return 1 / (1 + np.exp(-1. * x_v))
# 我们的Linear算子修改为一个class,并且在__call__方法中添加一个act参数,用来为线性层增加激活函数
class Linear(object):
def __init__(self, input_dim : int, output_dim : int, bias : bool = True, act : str = None):
self.input_dim = input_dim
self.output_dim = output_dim
if act and act not in _register_act_functions:
raise ValueError(f"input activate function '{act}' is not in registered activate function list:{list(_register_act_functions.keys())}")
self.act = act
self.W = Variable(np.random.randn(input_dim, output_dim))
if bias:
self.b = Variable(np.random.randn(1, output_dim))
def __call__(self, X : Node):
if not isinstance(X, Node):
raise ValueError("Linear's parameter X must be a Node!")
out = X @ self.W + self.b
if self.act:
act_func = _register_act_functions[self.act]
return act_func(out)
else:
return out
if __name__ == "__main__":
X = Placeholder()
fc = Linear(13, 1, bias=True, act="relu")
out = fc(X)
from pprint import pprint
pprint(_default_graph)
而在创建完图(_default_graph,计算图引用在一个全局变量里或类似的对象的成员里)后,我们需要跑图来完成一次前向运算和反向传播。而跑图需要基本函数run和其余的辅助函数我们会全部写在一个Session类中,也就是所谓的会话,会话类的run方法可以完成图的遍历和前向参数的更新。而反向传播的工作我们会交给优化器类Optimizer,有关反向传播获取指定节点(一般是损失值对应的节点)对于之前每个节点的梯度的方法和具体的优化方法迭代更新网络参数的逻辑会写在优化器类中。优化器类的minimize方法会帮助我们完成图的各个节点梯度表的获取和优化算法的参数更新。PS:因为不同的优化器算法要用到 这些成员。
纯Python实现原理级深度学习框架(二)前向运算和反向传播的实现,简单MLP实现boston预测
# create session to update nodes' data in the graph
class Session(object):
def run(self, root_op : Operation, feed_dict : dict = {}):
for node in _default_graph:
if isinstance(node, Variable):
node.data = np.array(node.data) # 本身的data就是data
elif isinstance(node, Placeholder):
node.data = np.array(feed_dict[node]) # 从输入的字典中获取对应的值
else:
input_datas = [n.data for n in node.input_nodes]
node.data = node.compute(*input_datas) # 获取其input_nodes的data,并作为参数送入Operation的compute方法中,compute返回的值就是Operation的data
return root_op
注册梯度函数:为了能够只通过函数名称就能关联到它所对应的梯度函数,添加一个_register_grad_functions,作为我们注册梯度函数的字典,接下来我们需要为每一个我们实现的Operation派生类写其对应的梯度函数,且这个梯度函数的注册名就是其对应的Operation派生类的类名。PS:此处的算子的bp方法注册有些麻烦,pytorch 思路类似于node class 既有compute 又有grad_fn。
class negative(Operation):
def __init__(self, x : Node):
super().__init__(input_nodes=[x])
def compute(self, x_v : np.ndarray):
return -1. * x_v
# negative对应的梯度函数,op_node为当前需要更新的节点的后继节点(所有节点的后继节点一定是Operation),grad为目标节点关于op_node节点值的梯度
@_register_grad_functions("negative")
def __negative_gradient(op_node : Operation, grad : np.ndarray):
return np.array([-1. * grad])
优化器
Optimizer只是一个基类,它会是所有具体的优化器(比如SGD,Adam,RMSprop等)的基类,因为这些优化器有许多的方法和变量成员是一样的,比如都需要BP来获取梯度值。所以此处,我将这些共性写入基类Optimizer中。其中的__backwards就是BP算法的实现,而minimize则是具体的优化算法实现的地方,对于基类,我们只需要实现__backwards,具体的优化逻辑(minimize方法)的实现就交给Optimizer的派生类吧。
# optimizer
class Optimizer(object):
def __init__(self, learning_rate : float = 1e-3):
"""
base for all the optimizer
"""
self.learning_rate = learning_rate
# BP算法的实现,大致过程是从目标节点(一般是损失函数节点,后面统称为loss节点)往前的一个BFS。
def __backwards(self, op_node : Operation):
"""
do the BP from the op_node,
return a gradient dict including op_node's gradients with respect to all the nodes before op_node
"""
grad_table = {} # 创建一个梯度字典,用来存放各个节点的梯度。
grad_table[op_node] = 1. # 首先将loss节点加入梯度字典中,值为1,毕竟自己对自己的梯度肯定是1嘛
visit_nodes = set()
queue = Queue()
visit_nodes.add(op_node)
queue.put(op_node)
while not queue.empty(): # 然后开始从loss往前BFS,在BFS的过程中,用当前节点的后继节点来更新该点的梯度值
cur_node = queue.get()
if cur_node != op_node:
grad_table[cur_node] = 0.
for next_node in cur_node.next_nodes:
grad_loss_wrt_next_node = grad_table[next_node] # loss gradient of next_node
next_node_op_name = next_node.__class__.__name__ # next_node must be an Operation, we get its name
gradient_func = _register_grad_functions[next_node_op_name] # get next_node's corresponding gradient function
grad_loss_wrt_cur_node = gradient_func(next_node, grad_loss_wrt_next_node) # call the gradient function to get the sub-gradient
if len(next_node.input_nodes) == 1: # if next_node represents monocular operators, then add to total gradient directly
grad_table[cur_node] += grad_loss_wrt_cur_node
else: # else get the portion size of gradient
cur_node_in_next_node_index = next_node.input_nodes.index(cur_node)
grad_table[cur_node] += grad_loss_wrt_cur_node[cur_node_in_next_node_index]
if isinstance(cur_node, Operation): # put next op node into queue to do the BFS
for input_node in cur_node.input_nodes:
if input_node not in visit_nodes: # only add nodes which haven't been updated/visited yet
visit_nodes.add(input_node)
queue.put(input_node)
return grad_table
# 优化算法实现的地方,会涉及到一些最优化的理论
def minimize(self, loss_node : Operation):
"""
concrete optimizer method,
this method will update parameters before "loss" node(include loss)
"""
pass
class SGD(Optimizer): # Stochastic gradient descent
def __init__(self, learning_rate : float = 1e-3):
super().__init__(learning_rate=learning_rate)
def minimize(self, loss_node : Operation):
lr = self.learning_rate
grad_table = self._Optimizer__backwards(op_node=loss_node)
for node in grad_table:
if isinstance(node, Variable):
grad = grad_table[node]
node.data -= lr * grad # 根据当前node 梯度更新当前 Variable node.data
return grad_table
PS:最上层是model.generate/model.forward,model 由多个layer构成,layer由Tensor运算构成,Tensor运算的过程中,通过魔术方法将node注册到graph,model.forward 即为graph 的拓扑排序遍历。Optimizer.backward 即为对 graph的bfs(调用的是每个node的gradient_func),得到一个grad_table。minimize 即为对grad_table 所有 Variable node 更新node.data = func(lr,grad)。
抽象层
组件抽象
神经网络运算主要包含训练 training 和预测 predict (或 inference) 两个阶段,训练的基本流程是:输入数据 -> 网络层前向传播 -> 计算损失 -> 网络层反向传播梯度 -> 更新参数,预测的基本流程是 输入数据 -> 网络层前向传播 -> 输出结果。从运算的角度看,主要可以分为三种类型的计算:(1)前向传递计算损失函数;(2)后向传递计算梯度;(3)优化器更新模型参数。:
- 数据在网络层之间的流动:前向传播和反向传播可以看做是张量 Tensor(多维数组)在网络层之间的流动(前向传播流动的是输入输出,反向传播流动的是梯度),每个网络层会进行一定的运算,然后将结果输入给下一层
- 计算损失:衔接前向和反向传播的中间过程,定义了模型的输出与真实值之间的差异,用来后续提供反向传播所需的信息
- 参数更新:使用计算得到的梯度对网络参数进行更新的一类计算
基于这个三种类型,我们可以对网络的基本组件做一个抽象
- tensor 张量,这个是神经网络中数据的基本单位
- layer 网络层,负责接收上一层的输入,进行该层的运算,将结果输出给下一层,由于 tensor 的流动有前向和反向两个方向,因此对于每种类型网络层我们都需要同时实现 forward 和 backward 两种运算。PS: layer就是内含了一系列参数、可被训练的单元,比如pytorch nn.Linear
- loss 损失,在给定模型预测值与真实值之后,该组件输出损失值以及关于最后一层的梯度(用于梯度回传)
-
optimizer 优化器,负责使用梯度更新模型的参数 然后我们还需要一些组件把上面这个 4 种基本组件整合到一起,形成一个 pipeline
- net 组件负责管理 tensor 在 layers 之间的前向和反向传播,同时能提供获取参数、设置参数、获取梯度的接口
- model 组件负责整合所有组件,形成整个 pipeline。即 net 组件进行前向传播 -> losses 组件计算损失和梯度 -> net 组件将梯度反向传播 -> optimizer 组件将梯度更新到参数。PS:一般框架都需要一个对象提供一个操作入口
基本的框架图如下图
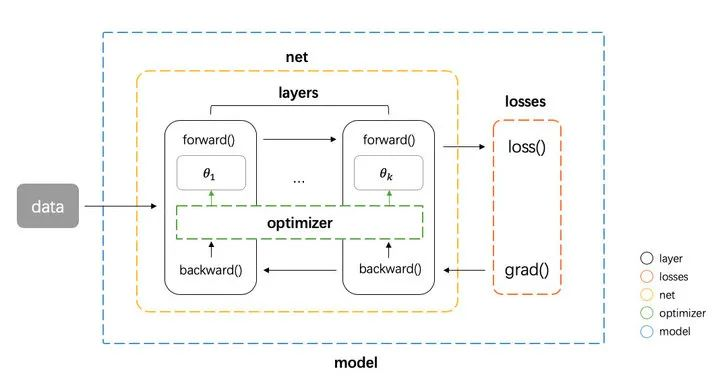
组件实现
按照上面的抽象,我们可以写出整个流程代码如下。PS:一个架构设计的典型案例
# define model
net = Net([layer1, layer2, ...])
model = Model(net, loss_fn, optimizer)
# training,将 net、loss、optimizer 一起传给 model,model 实现了 forward、backward 和 apply_grad 三个接口分别对应前向传播、反向传播和参数更新三个功能
pred = model.forward(train_X)
loss, grads = model.backward(pred, train_Y)
model.apply_grad(grads)
# inference
test_pred = model.forward(test_X)
tensor 张量是神经网络中基本的数据单位,我们这里直接使用 numpy.ndarray 类作为 tensor 类的实现。layer需要有提供 forward 和 backward 接口进行对应的运算。同时还应该将该层的参数和梯度记录下来。先实现一个基类如下
class Layer(object):
def __init__(self, name):
self.name = name
self.params, self.grads = None, None
def forward(self, inputs):
raise NotImplementedError
def backward(self, grad):
raise NotImplementedError
最基础的一种网络层是全连接网络层
class Dense(Layer):
def __init__(self, num_in, num_out,w_init=XavierUniformInit(),b_init=ZerosInit()):
super().__init__("Linear")
self.params = {
"w": w_init([num_in, num_out]),
"b": b_init([1, num_out])}
self.inputs = None
# forward 方法接收上层的输入 inputs,实现 的运算
def forward(self, inputs):
self.inputs = inputs
return inputs @ self.params["w"] + self.params["b"]
# backward 的方法接收来自上层的梯度,计算关于参数 和输入的梯度,然后返回关于输入的梯度
def backward(self, grad):
self.grads["w"] = self.inputs.T @ grad
self.grads["b"] = np.sum(grad, axis=0)
return grad @ self.params["w"].T
激活函数可以看做是一种网络层
class Activation(Layer):
"""Base activation layer"""
def __init__(self, name):
super().__init__(name)
self.inputs = None
def forward(self, inputs):
self.inputs = inputs
return self.func(inputs)
def backward(self, grad):
return self.derivative_func(self.inputs) * grad
def func(self, x):
raise NotImplementedError
def derivative_func(self, x):
raise NotImplementedError
net 类负责管理 tensor 在 layers 之间的前向和反向传播
class Net(object):
def __init__(self, layers):
self.layers = layers
# 按顺序遍历所有层,每层计算的输出作为下一层的输入
def forward(self, inputs):
for layer in self.layers:
inputs = layer.forward(inputs)
return inputs
# 逆序遍历所有层,将每层的梯度作为下一层的输入
def backward(self, grad):
all_grads = [] # 将每个网络层参数的梯度保存下来返回,后面参数更新需要用到
for layer in reversed(self.layers):
grad = layer.backward(grad)
all_grads.append(layer.grads)
return all_grads[::-1]
def get_params_and_grads(self):
for layer in self.layers:
yield layer.params, layer.grads
def get_parameters(self):
return [layer.params for layer in self.layers]
def set_parameters(self, params):
for i, layer in enumerate(self.layers):
for key in layer.params.keys():
layer.params[key] = params[i][key]
losses 组件需要做两件事情
class BaseLoss(object):
# 计算损失值
def loss(self, predicted, actual):
raise NotImplementedError
# 计算损失值和关于预测值的梯度
def grad(self, predicted, actual):
raise NotImplementedError
optimizer 主要实现一个接口 compute_step,这个方法根据当前的梯度,计算返回实际优化时每个参数改变的步长。
class BaseOptimizer(object):
def __init__(self, lr, weight_decay):
self.lr = lr
self.weight_decay = weight_decay
def compute_step(self, grads, params):
step = list()
# flatten all gradients
flatten_grads = np.concatenate([np.ravel(v) for grad in grads for v in grad.values()])
# compute step
flatten_step = self._compute_step(flatten_grads)
# reshape gradients
p = 0
for param in params:
layer = dict()
for k, v in param.items():
block = np.prod(v.shape)
_step = flatten_step[p:p+block].reshape(v.shape)
_step -= self.weight_decay * v
layer[k] = _step
p += block
step.append(layer)
return step
def _compute_step(self, grad):
raise NotImplementedError
model 类实现了我们一开始设计的三个接口 forward、backward 和 apply_grad
class Model(object):
def __init__(self, net, loss, optimizer):
self.net = net
self.loss = loss
self.optimizer = optimizer
def forward(self, inputs):
return self.net.forward(inputs)
def backward(self, preds, targets):
loss = self.loss.loss(preds, targets)
grad = self.loss.grad(preds, targets)
grads = self.net.backward(grad)
params = self.net.get_parameters()
step = self.optimizer.compute_step(grads, params)
return loss, step
def apply_grad(self, grads):
for grad, (param, _) in zip(grads, self.net.get_params_and_grads()):
for k, v in param.items():
param[k] += grad[k]
执行层
上面的抽象组件这么热闹,到真正的实现就又是另一幅天地了,可以好好品味 上层model 抽象与底层数据流图的gap,layer1 ==> layer2 ==> …layern 被展开成了 op,tenor 在layer 之间的流动 转换为了 dag op 间的流动。深度学习分布式训练的现状及未来AI 模型训练任务流程:初始化模型参数 -> 逐条读取训练样本 -> 前向、反向、参数更新 -> 读取下一条样本 -> 前向、反向、参数更新 -> … 循环,直至收敛。在执行层面的体现就是计算机按顺序运行一个个 OP。
几乎所有的 AI 框架都有 OP 的概念,简单来说就是一个函数,完成某个具体的功能,比如说加法、矩阵乘法、卷积等。为什么要多此一举引入这样一个概念呢?这其实是给每个具体计算功能抽象出一个统一接口,在静态图场景下能实现函数的编排(OP 的自由组合)。
Karpathy100行基于标量的自动微分引擎
Karpathy说,神经网络训练的核心是反向传播。其他的——优化算法、正则化、数据增强——都是效率问题。反向传播才是”一阶项”。所以micrograd项目,100行代码,只讲反向传播。一共两个py文件
- engine.py,一个标量值的自动求导引擎。实质是提供(仅)一个Value class,对应Pytorch.Tensor,提供了四则运算方法(神经网络就是一些四则表达式),反向传播机制
- nn.py,基于engine构建的神经网络库,定义了神经元(固定进行w *x + b运算)、神经元的层(特定个数的神经元)、多层感知机(输入输出层的尺寸、影藏层的尺寸和个数)。 这就是你理解神经网络需要的全部,其它的全是效率问题。
简单Tensor自动微分
动手学深度学习框架(4)- 手把手教你写一个功能完整的简易 Demo
#include <iostream>
#include <iomanip>
#include <string>
#include <unordered_map>
#include <random>
#include <chrono>
#include <any>
//自定义 Tensor 类型,这里数据成员非常简单,就是个标量,重载了基本数学运算符
class MyTensor {
public:
uint32_t data;
public:
MyTensor(){};
MyTensor(uint32_t x) : data(x) {}
MyTensor operator*(const MyTensor& a) {
this->data = this->data * a.data;
return *this;
}
MyTensor operator+(const MyTensor& a) {
this->data = this->data + a.data;
return *this;
}
MyTensor operator-(const MyTensor& a) {
this->data = this->data - a.data;
return *this;
}
MyTensor operator*(const int& a) {
this->data = this->data * a;
return *this;
}
};
// Op 基类
class OpBase {
public:
std::unordered_map<std::string, MyTensor> inputs;
std::unordered_map<std::string, MyTensor> outputs;
std::unordered_map<std::string, MyTensor> labels;
public:
virtual void Run() = 0;
};
// 乘法前向 Op
class MultipylyForward : public OpBase {
public:
void Run() {
MyTensor x = inputs["X"];
MyTensor w = inputs["W"];
MyTensor y1 = x * w;
outputs["Y"] = y1;
}
};
// 乘法反向 Op
class MultipylyBackward : public OpBase {
public:
void Run() {
MyTensor x = inputs["X"];
outputs["Y"] = x;
}
};
// 加法前向 Op
class AddForward : public OpBase {
public:
void Run() {
MyTensor x1 = inputs["X1"];
MyTensor x2 = inputs["X2"];
MyTensor y = x1 + x2;
outputs["Y"] = y;
}
};
// 加法反向 Op
class AddBackward : public OpBase {
public:
void Run() {
MyTensor x;
x.data = 1;
outputs["Y"] = x;
}
};
// loss 前向 Op,这里选取 MSE 作为示例
class LossForward : public OpBase {
public:
void Run() {
MyTensor y = inputs["X"];
MyTensor label = labels["Label"];
MyTensor loss = (y - label) * (y - label);
outputs["Y"] = loss;
}
};
// loss 反向 Op
class LossBackward : public OpBase {
public:
void Run() {
MyTensor y = inputs["X"];
MyTensor label = labels["Label"];
outputs["Y"] = (y - label) + (y - label);
}
};
// 梯度更新 Op
class UpdateGrad : public OpBase {
public:
double lr = 0.1;
std::unordered_map<std::string, MyTensor> inputs;
std::unordered_map<std::string, MyTensor> outputs;
public:
void Run() {
MyTensor w = inputs["W"];
MyTensor grad = inputs["Grad1"] * inputs["Grad2"] * inputs["Grad3"]; // 链式求导
MyTensor lr;
lr.data = this->lr;
outputs["Y"] = w - lr * grad;
}
};
int main() {
//1. 用户自定义前向组网
std::vector<std::string> program{"Multiply", "Add", "Loss"};
//2. 框架生成前向op + 自动补全反向OP + 插入梯度更新op
std::vector<std::string> ops{"multiply_forward", "add_forward", "loss_forward",
"loss_backward", "Add_forward", "multiply_backward", "update_grad"};
//3. 实例化 c++ 端 op 对象
std::vector<OpBase*> opClass {new MultipylyForward(), new AddForward(), new LossForward(),
new LossBackward(), new AddBackward(), new MultipylyBackward(), new UpdateGrad()};
//4. 框架根据用户组网,自动给每个op的输入赋值,这里仅以乘法前向op作个例子。一定要记住一点:框架中所有输入数据、
//参数、模型中间输入、输出、以及每个参数的梯度都有一个 string 类型的名字,它的存在是为了给op输入赋值服务的
opClass[0]->inputs["X"] = MyTensor(10);
opClass[0]->inputs["W"] = MyTensor(20);
for (auto op : opClass) {
op->Run();
}
//5. 测试第1个op的输出
std::cout << opClass[0]->outputs["Y"].data; // 输出结果:200
}
分布式
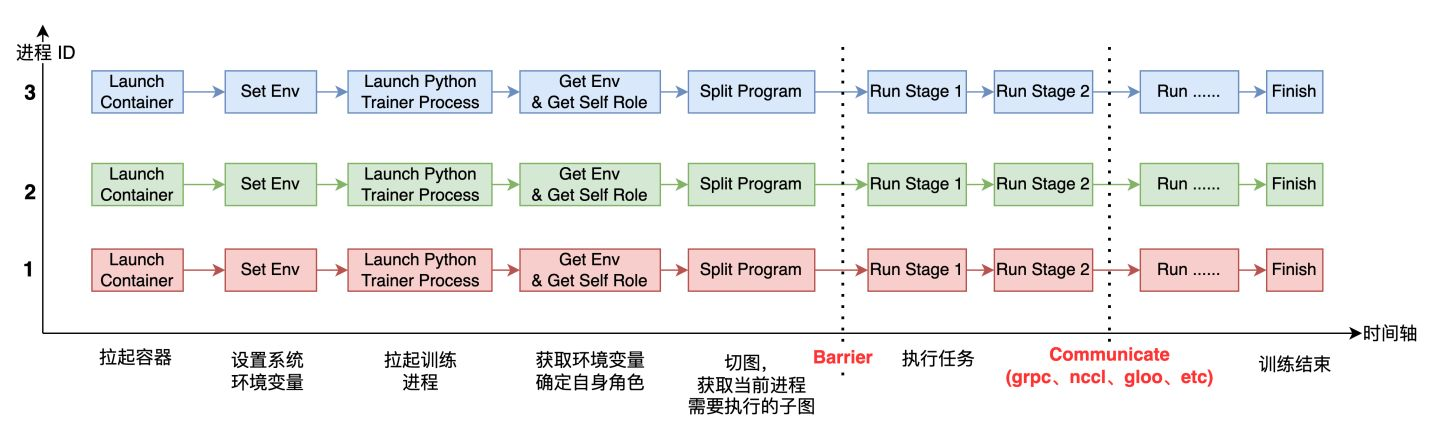
每个进程启动后,它需要感知自己全局的进程数( world_size)及自身的进程 ID(或者 rank_id),由于每个进程上运行的都是同一份训练脚本,所以得事先在每个进程所在的系统上设置不同的环境变量,进程运行起来之后,就可以获取环境变量,从而确定自己的角色(Worker、PServer、Coordinator 等)及rank_id、world_size 等信息。
在运行过程中,还有两个重要的环节是 Barrier 和 Communicate. Barrier 的目的是为了实现进程间同步,比较成熟的开源项目有 gloo、mpi 等。Communicate 操作就是实现通信,满足进程间数据交换需求。通信可以在同类型硬件之间发生,比如 CPU 到 CPU、GPU 到 GPU,也可以发生在不同硬件之间,比如 GPU 到 CPU,通信后端也有多种形式,比如 grpc、nccl、socket 等。
大模型时代
- 以前AI生态锚点主要是在AI框架的API上,丰富易用的API是AI框架被开发者广泛接受的基础,基于这些API开发的海量模型是整个生态系统的基础。在大模型时代,由于大模型超强的泛化性和大量的智能涌现的特征,特别是类ChatGPT语言大模型的出现,基于基础预训练模型的微调成为主流的模型开发模式,AI的生态锚点会从框架的API转移到预训练模型上;而且,大模型本身就是生态入口。例如ChatGPT、GPT-4等大模型,它甚至可以进行任务的规划和分解,这种能力根本无法通过传统模型实现。这种强大的能力会催生更多的产品和应用原生地长在这些大模型上,进而成为了AI框架的生态锚点。比如,AutoGPT项目,它可以接受用户设定的任务,然后通过GPT-4的能力进行任务的分解,并协同其他工具完成用户设定的任务。AutoGPT三月份开源,目前Star数量已经超过了13万。
- 规模都超过千亿参数,甚至达到了万亿参数规模,训练这些大模型往往需要用到千张加速卡集群,从零开始训练的周期也是以月为单位计数。而从大模型的发展趋势来看,模型的参数可能还会持续增长,但是底层芯片的算力增长速度功能已经远落后于模型参数,导致模型规模和算力规模之间出现鸿沟,而这个鸿沟需要AI框架进行弥补,这很大程度上会使得AI框架关注的重点再次回到运行效率和可靠性上
- 静态图重新占有优势,在超大规模集群上,动态图并不能比静态图有更好的易用性,相反静态图有更好的性能和内存使用率,这个与小模型是不一样的。
- 大模型的分布式并行切分变得更加关键,从大模型训练的角度,如何提高上千张加速卡的运行效率?核心问题是通过编程将几千亿的模型参数合理的划分到这些加速卡上,并尽可能减少通信和内存搬移开销,这就需要框架支持灵活的并行切分模式;另外,如果这个过程全部靠工程师手动编程,则需要耗费大量的时间对系统性能进行调试调优,即使大模型发展这么久了,参与大模型工作的系统优化方面的工程师仍然至少占到1/3以上,这个问题的关键挑战是如何简化分布式编程的复杂度,使得工程师可以像单机编程一样,为分布式AI集群编程。为此,需要重点解决三个方面的问题:
- 支持足够多的并行策略,满足各种大模型高效训练的要求;
- 通过感知模型和硬件全局信息,做到全局配置优化;
- 在合理时间内能够自动搜索并生成能够最高的分布式并行策略,减少人工编程和调优的开销。
- 分布式并行训练长稳运行的必要性:在千卡集群中,硬件失效是常态,如何保证系统稳定可靠的运行,即便有硬件失效,也能快速恢复,就成为一个关键的能力。
- AI推理需要解决端侧部署大模型的挑战。由于大模型需要消耗大量的计算和内存资源,现有的大模型基本都是基于云环境提供服务,这会限制大模型的应用场景。比如,在端侧,很多涉及用户隐私的任务是无法发回到云环境执行的,这会导致大模型在ToC业务场景中受限。大模型在端侧的部署和应用主要有两种方式:
- 端侧部署的大模型独立完成任务,虽然有一些方法能让大模型在端侧跑起来,但是占用的内存和计算资源可能会影响其他应用,同时压缩后的模型的效果也没有经过全面的测试,能够支撑的使用场景应该是有限的。
- 通过端侧和云侧的协同将大模型的能力应用在端侧。在端侧对用户的请求做初步处理,将更加复杂的任务发挥到云侧大模型去执行,这种模式下,推理时延的优化尤为重要。
推荐文章
动手学深度学习框架(1) - AI 模型是如何训练出来的 写的很不错。
- BIDMach的整体设计分三层,下层关注于底层硬件的性能并统一封装为矩阵运算和Actor间的通信操作;中间层是各种机器学习算法的计算图封装,而最上层则是面向用户设计的交互式机器学习工具。
- 一般来说,类似tensorflow/pytorch这样的深度学习框架,实际上是提供了一个可微计算图引擎,他们可以非常方便地构建一个可微的函数(如下图所示),然后基于数据去最小化损失函数,这种抽象使得深度学习变得非常简单和可行易用。但是到了工业界(搜索/推荐/广告),实际的机器学习问题远不止这么简单,我们要重新思考一下框架的职责。框架是只需要专注于做损失函数优化就可以呢?还是会有很多其它事情也要去负责呢?
- 比如图中所示的x、y样本数据本身的生成就是一个很大的问题:比如样例生成或者特征萃取。而且在互联网应用中,我们往往需要从流式的数据流中实时地完成x、y的生成。
- 到了工业界中,训练和推理很可能是要被分开去做的。因为在推理的时候你只需要处理一个固定的计算图,这就存在很多优化的空间。
所以实际情况是,如果把框架的概念从一个单点应用扩展到一个可用的工业界框架后,就会包含很多模块:样本的处理、特征的处理、离线训练和在线推理,各种数据接口,一致性保障、资源管理和整个实验平台等等一系列工具。这些东西可能从广义来讲都算是框架中的一部分。
- 框架与算法共同进化。工程框架的发展是跟整个算法的红利包括跟整个业务的发展都有关联的。算法侧提出了一个新的结构,框架就需要去做适配和推理优化。框架的革新又会导致算法工程师可以去尝试更复杂更加有意思且更有深度的想法。整个过程就是一个共同进化共同演化的过程。
深度解析开源推荐算法框架EasyRec的核心概念和优势针对推荐流程的各个阶段,业界已经有很多的模型,这些模型大部分也有开源的实现,但是这些实现通常散落在Github的各个角落,其数据处理和特征构造的方式各有差异。如果我们想要在一个新的场景里面应用这些模型,通常需要做比较多的改动:
- 输入的改造,开源的实现的输入格式和特征构造通常和线上不一致,适配一个算法通常需要1-2周左右的时间,还难免因为对代码的不熟悉引入bug,如果要尝试5个算法的话,就需要5倍的改造时间。如果算法资源有限,这时候是不是就要忍痛割爱,放弃一些可能有效果的尝试了?
- 开源的实现很多只是在公开数据集上取得了比较好的效果,在公开数据集上的最优参数也不一定适合实际的场景,因此参数调优也需要较大的工作量;如果没有系统化的调参方法,很多算法也就是简单试一下,没有deep explore,哪来对算法的深入理解呢? 为什么看似简单的改进,你没有能够发现呢?
- 开源的实现用的是TensorFlow 1.4,而线上用的TensorFlow 2.3,好多函数的参数都变掉了
- 费了九牛二虎之力把模型效果调好了,发现上线也会有很多问题,比如训练速度太慢、内存占用太大、推理qps跟不上、离线效果好在线效果跪等等。
遇到这么多问题,你还有精力去做你的下一个idea吗?你还能斗志昂扬,坚持不懈的去探索新方向吗?刘童璇:阿里巴巴稀疏模型训练引擎DeepRec 可以学习针对稀疏场景如何去优化tensorflow。