简介
MLP 只是理论上可以拟合所有的函数,但是复杂场景,可能需要提前设计超级深的隐藏层为代价(深了会有两个问题,怎么加快训练让模型收敛,模型很容易梯度消失)。这样无异加重了计算量,所以一般不这么直接搞。一般会提前提取一下特征,让MLP模型学精华就好了。我们是用一个新的模型(可能是一个 MLP?)做特征的学习,期望它自己学习到特征的表示,所以我们称之为表征学习(Representation Learning), 表征的直观形式就是一个 embedding。
- 图片表征。假设原始数据是一张图片,模型怎么学到图片里面的特征呢,比如有天空正在下着雪,雪下有一个湖,湖心有个亭子,湖中人鸟声俱绝,而我们正在亭中一边看雪,一边拿着毛笔写文章《湖心亭看雪》。这其实一直都是 CNN(卷积神经网络) 在解决的问题,我们不用去理解每一层做了什么,只明白一个道理,原始图片到最后的全连接层(MLP) 中间的这几层是在做特征的提取,最终学到特征的正确表达,就是我们说的表征学习。
- 文本表征。
- word2vec
- transformer,第一步特征工程,one-hot,然后把特征数据输入到 self-attention中做表征学习。学完之后输出到到 MLP 中学习,MLP 的最后一层的节点个数是词表的大小,其表达未归一化的分数,这些分数被称为 logits(logit蒸馏就是让 student模型学到这个数据分布),最后借助 softmax判断每个词的概率,最后选择概率最高的那个 token。
- 图谱表征。GCN
- 如何处理时序?单独用 MLP 其实处理不了时序数据。
- RNN就一个一个 token 喂给模型 这是深度学习的一个重要范式,可以总结为 embedding+MLP,有了这个范式我们就可以分别去做优化了。提升embedding的准确性,并开发一个强大的模型以进行有效学习。直观地说,就是要将更多的知识以最高质量的形式融入到一个更强大、参数更多的模型中,让其学到更多,做的更好。有了这个 embedding,其实可以单独用的,可以放在向量数据库中,就可以做向量相似度召回,比如有了句子的 embedding 就可以提供一个 RAG 方案了。
脉络:传统神经网络或CNN ==> 解决输入输出不固定的问题引入RNN ==> 解决M to N问题引入编码集-解码器(两个RNN+context) ==> 为了避免相同的上下文变量对模型性能的限制,给编码器-解码器模型加入了注意力机制 ==> 如何计算注意力?自注意力——Transformer。
要解决的一类问题:Seq2Seq模型
我们通常处理的信息有声音、图片、文字。而这三种信息,很容易想到的,可以转换成一个向量组,也就是一个序列(sequence)。,一般来说,我们把一个单词/片段等称为一个token。seq问题可以大致分为两大种类,输入输出相同token数和输入输出不同token数。
Seq2Seq模型可以认为是一个序列到序列转换的通用框架(序列转换架构),具有广泛的应用场景,可以完成诸如“中文->英文”的翻译任务,也可以完成“文章->关键词”的摘要提取任务,甚至可以完成“图像->文字”的看图说话任务。然而,Seq2Seq模型的编码器-解码器架构也存在着明显的缺陷。
- Seq2Seq模型理论上可以接受任意长度的序列作为输入,但是机器翻译的实践表明,输入的序列越长,模型的翻译质量越差。产生这一问题的原因在于无论输入序列的长短,编码器都会将其映射为一个具有固定长度的上下文序列c。这就意味着当输入序列的长度过长时,上下文序列将无法表示整个输入序列的信息。试想在一个文本摘要生成的应用中,若c为一个几百维的向量,在针对一段短新闻稿时,也许能够表达新闻稿的全部语义信息,但是面对一篇长篇小说,恐怕其在语义信息表达方面将显得力不从心。
- 在上述编码器-解码器框架中,在生成每一个目标元素$y_i$时使用的下文序列c都是相同的,这就意味着输入序列x中的每个元素对输出序列y中的每一个元素都具有相同的影响。换句话说,解码阶段不同时间步看到的输入序列的信息都是一样的,这种现象是有悖常理的。毕竟在一个输入序列中,不同元素所携带的信息量是不同的,受到关注的程度也自然存在差异。例如在英文到中文的机器翻译应用中,英文语句中的不定冠词“a”或“an”在很多场合是不需要显式翻译的,而类似“very”这样的副词在很多语句中却携带着很重的情感信息。
为什么要发明循环神经网络
为什么提出RNN?或者传统神经网络或CNN 为什么不行?传统的神经网络,以及CNN,它们存在的一个问题是,采用固定的大小的输入并产生固定大小的输出(input是一个固定大小的向量)。而RNN呢?比如处理文本,其输入和输出的长度是可变的(input是一个不固定长度的多个向量,一个向量代表一个词),比如,一对一,一对多,多对一,多对多。
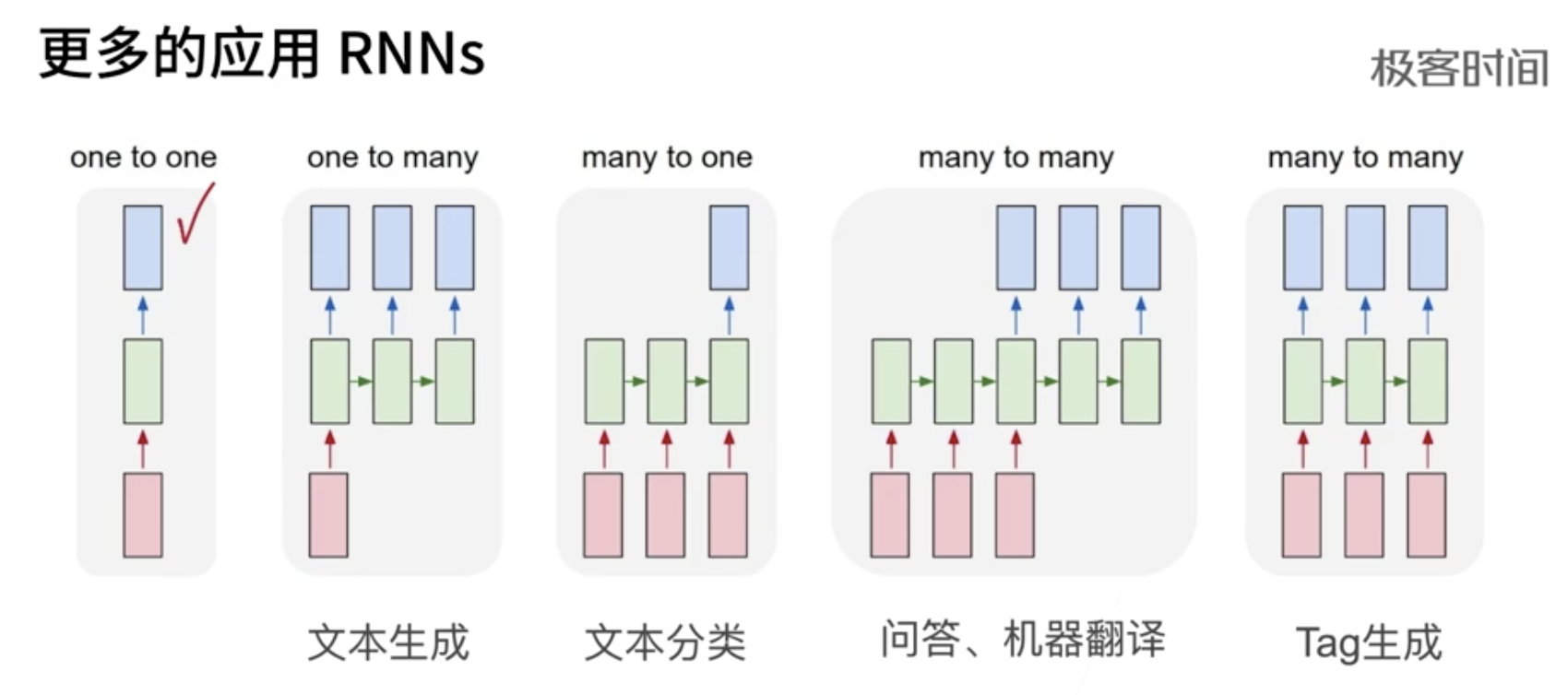
RNN是神经网络中的一种,它的链状结构,擅长对序列数据进行建模处理。序列数据有很多种形式。音频是一种自然的序列,你可以将音频频谱图分成块并将其馈入RNN。文本也是一种形式的序列,你可以将文本分成一系列字符或一系列单词。
- 循环神经网络,引入状态变量来存储过去的信息,并用其与当期的输入共同决定当前的输出。 多层感知机 + 隐藏状态 = 循环神经网络
- 应用到语言模型中时 ,循环神经网络根据当前词预测下一时刻词
- 通常使用困惑度来衡量语言模型的好坏
RNN 输入和输出 根据目的而不同
- 比如 根据一个字预测下一个字,输入就是一个字的特征向量(后续就是这个字的某个数字编号)
- 给一个词 标记是名词还是动词
- 语音处理。输入一个每帧的声音信号 的特征向量
RNN 结构
史上最详细循环神经网络讲解(RNN/LSTM/GRU)先来看一个NLP很常见的问题,命名实体识别,举个例子,现在有两句话:
- 第一句话:I like eating apple!(我喜欢吃苹果!)
- 第二句话:The Apple is a great company!(苹果真是一家很棒的公司!)
现在的任务是要给apple打Label,我们都知道第一个apple是一种水果,第二个apple是苹果公司,假设我们现在有大量的已经标记好的数据以供训练模型,当我们使用全连接的神经网络时,我们做法是把apple这个单词的特征向量输入到我们的模型中,在输出结果时,让我们的label里,正确的label概率最大,来训练模型。
// 序列模型的X 和 Y,实际上一般是随机采样,每个样本都是在原始的长序列上任意捕获的子序列。基于所有词会创建一个词表,每个词由其在词表中的位置 对应的向量来表示。
// features ==> labels
I like ==> eating
like eating ==> apple
the apple ==> is
apple is ==> a
is a ==> greate
a greate ==> company
但我们的语料库中,有的apple的label是水果,有的label是公司,这将导致,模型在训练的过程中,预测的准确程度,取决于训练集中哪个label多一些,这样的模型对于我们来说完全没有作用。问题就出在了我们没有结合上下文去训练模型
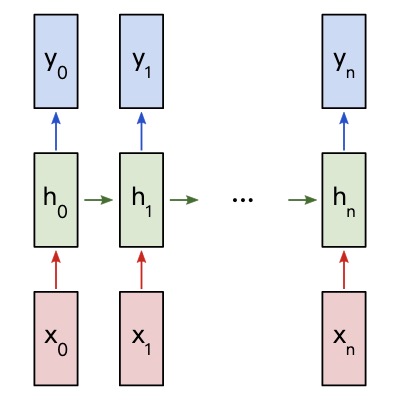
- 「输入层」:X是一个向量,它表示「输入层」的值,并且与隐藏层之间不是全连接,而是按照时刻进行与隐藏层之间进行对齐连接。
- 「隐藏层」:h是一个向量,它表示「隐藏层」的值(节点数与向量S的维度相同);
- 「输出层」:y是一个向量,它表示「输出层」的值;
RNN 输出$y_i$依赖于上一个状态$h_{i-1}$和当前输入$x_i$所推导出的隐状态$h_i$,这种机制在解决了传统神经网络无法与过去输入建立联系的问题。与多层感知机 (MLP) 等前馈网络不同,RNN 有一个内部反馈回路,负责记住每个时间步的信息状态。
RNN Cell(RNN 就是一个RNN Cell 的不断复制):a typical vanilla RNN uses only 3 sets of weights to perform its calculations: $W_{xh}$,$W_{hh}$,$W_{hy}$。 We’ll also use two biases for our RNN: $b_h$,$b_y$。
\(h_t = tanh(W_{xh}x_t + W_{hh}h_{t-1} + b_h)\) \(y_t = W_{hy}h_t + b_y\)
rnn 是通过 $W_{hh}$ 存储时序信息的。
RNN 代码
rnn = RNN()
ff = FeedForwardNN()
hidden_state = [0.0,0.0,0.0,0.0]
for word in input:
output , hidden_state = rnn(word, hidden_state)
...
prediction = ff(output)
An Introduction to Recurrent Neural Networks for Beginners RNN 的前向 后向传播等,并给出了一个基于文本给出情感的例子,很仔细。PS: forward 和 backward 有点从左到右 和 从右向左的意思。
class RNN:
# A Vanilla Recurrent Neural Network.
def __init__(self, input_size, output_size, hidden_size=64):
# Weights
self.Whh = randn(hidden_size, hidden_size) / 1000
self.Wxh = randn(hidden_size, input_size) / 1000
self.Why = randn(output_size, hidden_size) / 1000
# Biases
self.bh = np.zeros((hidden_size, 1))
self.by = np.zeros((output_size, 1))
def forward(self, inputs):
'''
Perform a forward pass of the RNN using the given inputs.
Returns the final output and hidden state.
- inputs is an array of one-hot vectors with shape (input_size, 1).
'''
h = np.zeros((self.Whh.shape[0], 1))
# Perform each step of the RNN
for i, x in enumerate(inputs):
h = np.tanh(self.Wxh @ x + self.Whh @ h + self.bh)
# Compute the output
y = self.Why @ h + self.by
return y, h
def forward(self, inputs):
'''
Perform a forward pass of the RNN using the given inputs.
Returns the final output and hidden state.
- inputs is an array of one-hot vectors with shape (input_size, 1).
'''
h = np.zeros((self.Whh.shape[0], 1))
self.last_inputs = inputs
self.last_hs = { 0: h }
# Perform each step of the RNN
for i, x in enumerate(inputs):
h = np.tanh(self.Wxh @ x + self.Whh @ h + self.bh)
self.last_hs[i + 1] = h
# Compute the output
y = self.Why @ h + self.by
return y, h
在 RNN 里面,给一个序列,它的计算是把这个序列 从左往右 一步一步往前做。假设一个序列是一个句子,它就是一个词一个词的看。对第 t 个词,它会计算一个输出叫做$h_t$(该词 的隐藏状态),然后该词的$h_t$是由 前面一个词的隐藏状态$h_{t-1}$和当前 第 t 个词本身决定的。这样它就可以把前面学到的历史信息通过$h_{t-1}$放到当下,然后和当前的词 做一些计算 得到输出。这也是 RNN 为何能够有效处理时序信息的一个关键所在。它把之前的信息全部放在隐藏状态里面,然后一个一个循环下去。但它的问题也来自于此
- RNN 是一个时序一步一步计算的过程,比较难以并行。就是说在算 第 t 个词的时候,算出 $h_t$的时候,必须要保证 前面那个词的$h_{t-1}$输入完成。假设 句子有 100 个词的话,那么需要 时序的算 100 步,导致说在这个时间上,无法并行。现在GPU 都是成千上万个线程,无法在这个上面并行的话,导致 并行度比较低,使得在计算上性能比较差。
- 历史信息是一步一步的往后传递的,如果 时序比较长的话,那么 很早期的那些时序信息,在后面的时候可能会丢掉,如果不想丢掉的话,那可能得要$h_t$比较大。但是问题是:如果$h_t$比较大,在 每一个时间步 都得把它存下来,导致内存开销是比较大。
GRU 和 LSTM
RNN网络对任意时刻的输入都是赋予相同权重计算,这样区分不出重点因素。可以进行一个短期的记忆,长期记忆的实现一般使用LSTM模型,当预测点与依赖的相关信息距离比较远的时候,就难以学到该相关信息。例如在句子“我是一名中国人,…….(省略数十字),我会说中文”,如果我们要预测末尾的“中文”两个字,我们需要上文的“中国人”,或者“中国”。
GRU: 能关注的机制(更新门/Zt),能遗忘的机制(重置门/Rt)。PS:多了几个要学习的weight。
\(R_t = \sigma(X_tW_{xr} + H_{t-1}W_{hr}+b_r)\) \(Z_t = \sigma(X_tW_{xz} + H_{t-1}W_{hz}+b_z)\) \(\tilde{H_t} = tanh(X_tW_{xh}+(R_t\bigodot H_{t-1})W_{hh+b_h})\) \(H_t = Z_t \bigodot H_{t-1} + (1-Z_t) \bigodot \tilde{H_t}\)
$\bigodot$ 是按元素乘法的意思,比如$R_t$ 全是0 ,则$H_{t-1}$ 就几乎无效了。
由于 RNN 自身的结构问题,在进行反向传播时,容易出现梯度消失或梯度爆炸。LSTM 网络在 RNN 结构的基础上进行了改进,通过精妙的门控制将短时记忆与长时记忆结合起来,一定程度上解决了梯度消失与梯度爆炸的问题。
Encoder-Decoder/两个RNN加context
NLP注意力机制的视觉应用——谈谈看图说话的SAT模型由于结构上的受限,RNN只能实现“1 to N”、“N to 1”和“N to N”的形式。那么对于“M to N”这种形式的句子关系(输入输出不等长问题,如机器翻译、阅读理解等场景),RNN便显得有些乏力。于是,大佬们提出了Seq2Seq,这是一个拥有编码器Encoder和解码器Decoder的模型,其中,Encoder和Decoder都是RNN类型的网络,上下文变量(thought vector)为二者搭建起了信息传递的桥梁,编码器将输入序列的信息编码到上下文变量中,解码器将上下文变量中的信息解码生成输出序列。依靠“意义”这一中介,Seq2Seq成功解决了两端语句单词数量不对等的情况,即与传统RNN模型相比,更好的解决了“M to N”。
编码器-解码器的设计是多种多样的,需要根据具体问题具体分析。编码器获取输入并将其编码为固定长度的向量,而解码器获取该向量并将其解码为输出序列。编码器和解码器联合训练以最小化条件对数似然。一旦训练完毕,编码器/解码器就可以在给定输入序列的情况下生成输出,或者可以对成对的输入/输出序列进行处理。比如在中译英任务中,编码器会将输入序列从源空间(例如中文)投影到一个高维语义空间的向量表示中。接着,解码器将这个高维向量从语义空间映射回目标空间(例如英文),生成一个新的序列作为翻译输出。只是在做各个语义空间中的相互投影罢了,只不过这个投影的方法叫做编码器和解码器。
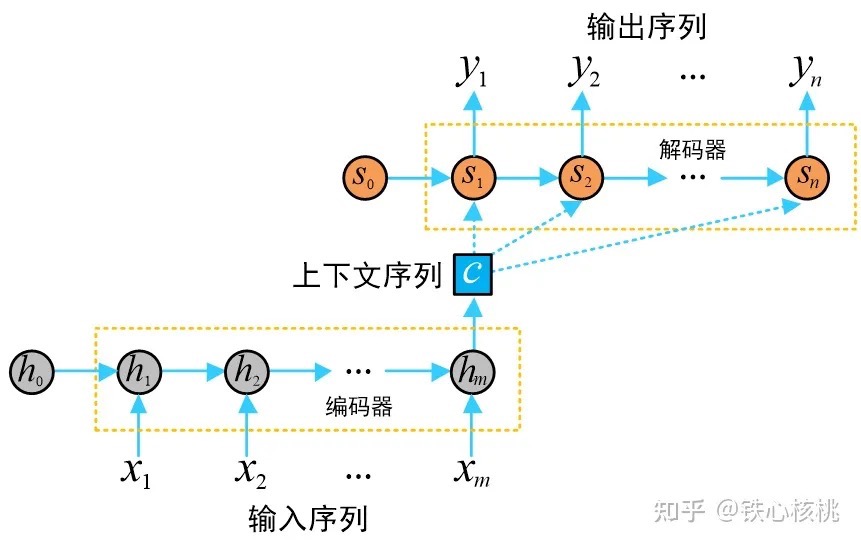
编码器实现将输入的任意长度的输入序列x映射为固定长度的上下文序列 c(PS:有的地方理解为embedding),该上下文序列为输入序列的一个中间编码表示 $c = Encoder(x_1,…,x_m)$
获得c的具体方法有多种
- 可以取RNN编码器的最后一个隐状态,即 $c=h_m$
- 可以是最后一个隐状态的某种变换,即$c=q(h_m)$
- 可以对针对所有隐状态做的某种变换,即 $c=q(h_1,h_2,…h_m)$ 解码器用来将上述固定长度的中间序列c映射为变长度的目标序列作为最终输出 ,其中输出序列中的每一个元素$y_i(i=1,2,…,n)$依赖中间序列c 以及其之前的隐状态,即$y_i=Decoder(c,s_1,s_2,…,s_{i-1})$。$s_i$ 是decoder的隐藏状态。
解码器跟编码器的不一样的是:在解码器里面,词是一个一个生成的。对编码器来讲,很有可能是一次性看全整个句子,比如做机器翻译的时候,可以把整个英语的句子给你。但是在解码的时候,只能一个一个的生成,这个东西叫做一个叫做自回归(auto-regressivet),在自回归里面,模型的输入又是模型的输出。
具体来说,在最开始给定 z,那么要去生成第一个输出$y_1$,拿到$y_1$之后,就可以去生成$y_2$。一般来说要生成$y_t$,可以把之前所有的 $y_1$到$y_{t-1}$全部拿到。也就是说在机器翻译的时候是一个词一个词地往外蹦,所以在过去时刻的输出,也会作为当前时刻的输入,所以这个叫做自回归。
注意力机制/抛弃RNN
为什么需要注意力机制?解决的是在预测下一个词时,要理解上下文的关系,才能更好的预测下一个词,让模型表现更好。
CNN和RNN已经具备通过神经网络实现分类、预测能力,但是存在两个典型问题:
- CNN聚焦局部信息,丢失全局信息。Encoder 阶段需要把所有信息都要压缩到固定长度的向量中,由于串行处理的梯度消失问题,RNN 无法捕捉到长距离的依赖关系。
- RNN无法并行计算(串行模式理论上确实也可以做到窗口无限大,然后从左到右把全部信息带过来,效率太差)。
从RNN到“只要注意力”——Transformer模型基于RNN的架构存在着一个明显弊端,那就是RNN属于序列模型,需要以一个接一个的序列化方式进行信息处理,注意力权重需要等待序列全部输入模型之后才能确定,即需要RNN对序列“从头看到尾”。这种架构无论是在训练环节还是推断环节,都具有大量的时间开销,并且难以实现并行处理。例如面对翻译问题“A magazine is stuck in the gun.”,其中的“magazine”到底应该翻译为“杂志”还是“弹匣”?当看到“gun”一词时,将“magazine”翻译为“弹匣”才确认无疑。在基于RNN的机器翻译模型中,需要一步步的顺序处理从magazine到gun的所有词语,而当它们相距较远时RNN中存储的信息将不断被稀释,翻译效果常常难以尽人意,而且效率非常很低。我们不禁要问一个问题:RNN 结构是否真的必要?谷歌大脑、谷歌研究院等团队于 2017 年联合发表文章《Attention Is All You Need》,给出了的答案——“RNN is unnecessary, attention is all you need”。PS:为什么RNN上下文理解能力弱?因为RNN通过一个隐藏层记录当前及之前所见过的词汇,已经将语义信息杂糅在一起,而往往理解 it 这个词的语义时候,通过几个词就行,而不是it 之前的所有词汇。在“A magazine is stuck in the gun.” 这句里,我们希望对 magazine 编码为一个向量,它和gun 向量的距离更近。
Transformer 沿用了经典的 Encoder-Decoder 结构,但完全摈弃了传统的循环结构,Encoder 的任务是理解输入序列,将其转换为富含上下文信息的特征表示,编码器由多个相同的层(layers)堆叠而成,每一层都包含两个主要的子层:自注意力+前馈神经网络。自注意力机制让每个位置都能”看到”序列中的所有其他位置。以句子”The cat sat on the mat”为例:理解”cat”时,模型会关注”The”(确定是哪只猫),理解”sat”时,模型关注”cat”(谁在坐)和”on the mat”(坐在哪里)。在每个子层周围都使用了残差连接(Residual Connection)和层归一化(Layer Normalization),以帮助模型更稳定地进行训练。通过这一系列操作,编码器能够逐步提炼输入序列的表示,为解码器生成目标序列提供全面的上下文信息。
深度学习中的“注意力”概念源于改进循环神经网络(RNN)使其能够处理较长序列或句子,例如,将句子从一种语言翻译成另一种语言。我们通常不会选择逐字翻译,因为这种方式忽略了每种语言特有的复杂语法结构和惯用表达,会导致翻译不准确或无意义。为克服上述问题,引入了注意力机制,允许模型在每个时间步都能够访问所有序列元素。注意力机制的关键在于选择性地确定在特定上下文中哪些词语是最重要的。
对于一个由 n 个单词组成的句子来说,不同位置的单词,重要性是不一样的。因此,我们需要让模型“注意”到那些相对更加重要的单词,这种方式我们称之为注意力机制,也称作 Attention 机制。比如“我今天中午跑到了肯德基吃了仨汉堡”。这句话中,你一定对“我”、“肯德基”、“仨”、“汉堡”这几个词比较在意,不过,你是不是没注意到“跑”字?其实 Attention 机制要做的就是这件事:找到最重要的关键内容。它对网络中的输入(或者中间层)的不同位置,给予了不同的注意力或者权重,通过权重矩阵来自发地找到token之间的关系,网络就可以逐渐知道哪些是重点,哪些是可以舍弃的内容了。
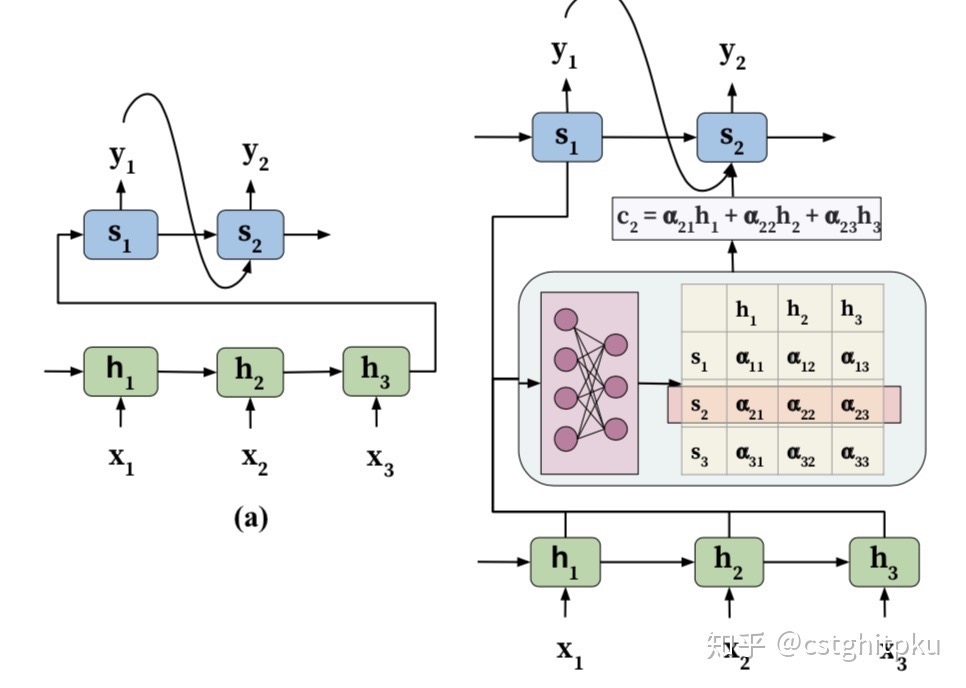
与标准Seq2Seq模型相比,注意力模型最大的改进在于其不再要求编码器将输入序列的所有信息都压缩为一个固定长度的上下文序列c中,取而代之的是将输入序列映射为多个上下文序列$c_1,c_2,…,c_n$,其中$c_i$是与输出$y_i$对应的上下文信息。
下图示意了一个注意力模型的基本结构,其中的注意力模块可以视为是一个具有m个输入节点和n个输出节点的全连接神经网络。PS:Attention 可以看做为解码器阶段的每个单元,单独准备了一个定制、全局的 C。
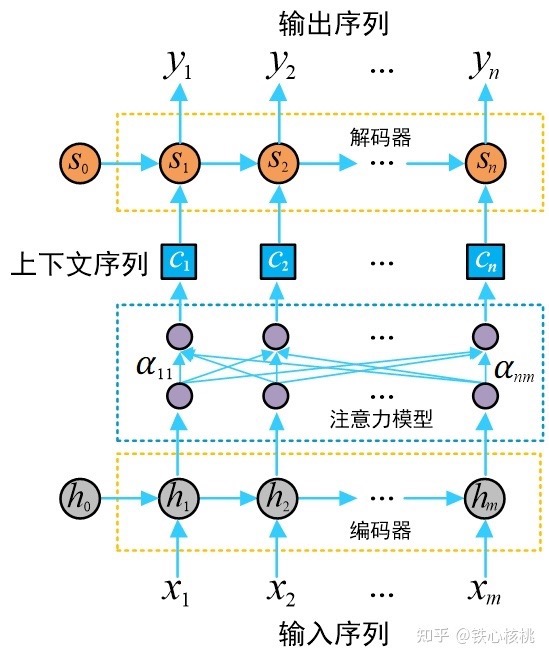
在注意力模型中,每一个上下文序列为编码器所有隐状态向量的加权和
\[c_i=\sum_{j=1}^m\alpha_{ij}h_j\]其中$\alpha_{ij}$为注意力权重系数(也称为注意力得分)。在编码器中,隐变量$h_j$蕴含了输入序列第j个元素的信息,因此对编码器隐变量按照不同权重求和表示在生成预测结果$y_i$时,对输入序列中的各个元素上分配的注意力是不同的——$\alpha_{ij}$越大,表示第i个输出在第j个输入上分配的注意力越多,即生成i个输出时受到第j个输入的影响也就越大,反之亦反。
剩下最后一个问题即如何得到注意力权重系数$\alpha_{ij}$了。在注意力模型中,注意力权重系数是通过构造一个全连接网络,然后再对该网络输出向量进行概率化得到的。这个参考原文。
小结:为模型的每一个输入项(比如语句中的某个单词)分配一个权重,这个权重的大小就代表了我们希望模型对该部分一个关注程度。这样一来,通过权重大小来模拟人在处理信息的注意力的侧重,有效的提高了模型的性能,并且一定程度上降低了计算量。PS:注意力机制本质上就是学习/更新权重,训练完后,权重大的地方被关注了,权重小的地方被轻视。注意力实际上是“关注输入数据中最重要的部分”。从技术上讲,注意力测量两个向量之间的“相似度”,并返回“加权相似度分数”。
Attention 另一种表述
QKV视角
Attention 机制最先源于计算机视觉领域,其核心思想为当我们关注一张图片,我们往往无需看清楚全部内容而仅将注意力集中在重点部分即可。而在自然语言处理领域,我们往往也可以通过将重点注意力集中在一个或几个 token,从而取得更高效高质的计算效果。Attention 机制有三个核心变量:Query(查询值)、Key(键值)和 Value(真值)。
我们可以通过一个案例来理解每一个变量所代表的含义。 例如,当我们有一篇新闻报道,我们想要找到这个报道的时间,那么,我们的 Query 可以是类似于“时间”、“日期”一类的向量 (为了便于理解,此处使用文本来表示,但其实际是稠密的向量), Key 和 Value 会是整个文本。通过对 Query 和 Key 进行运算我们可以得到一个权重, 这个权重其实反映了从 Query 出发,对文本每一个 token 应该分布的注意力相对大小。 通过把权重和 Value 进行运算,得到的最后结果就是从 Query 出发计算整个文本注意力得到的结果。具体而言,Attention 机制的特点是通过计算 Query 与Key的相关性为真值加权求和, 从而拟合序列中每个词同其他词的相关关系。PS:注意力机制可以描述为将query 和一系列的 key-value 对映射到某个输出的过程,而这个输出的向量就是根据 query 和 key 计算得到的权重作用于 value 上的权重和。在搜索引擎的例子中,往往作为你搜索的内容,是从网页中提取的关键信息(比如index,而不是内容本身),而Value则是实际页面的内容。一个非“机器”的例子是去找出一群学生中的“优秀学生”,此时“优秀学生标准”作为查询 ,而学生的成绩可能被(粗暴并充满争议地)定义为查询试图匹配的指标 ,通过与的组合去关注到相应的学生 。另外一类例子则更像是对信息的一种重组:假定你现在遇到一件令你头疼的事情,你对此求助了多个人,每个人都给出了不同的意见。而你最后做出的决定,可能并不严格遵循任何人的意见——而是以你的问题为Q,你求助的人在这个问题上可能扮演的角色K,你会对每个人给出不同的信任。而你的最终方案,可能参考了所有人的意见——但是针对这种信任的不同,每个人的意见在你的最终方案中的分量也是不同的。
初学者最困惑的一个问题就是Q、K和V分别是怎么来的?Q、K 和 V 其实就是输入 X 分别乘以 3 个不同的矩阵计算而来,可以理解为这是对于同一个输入进行 3 次不同的线性变换来表示其不同的 3 种状态。在计算得到Q、K、V之后,就可以进一步计算得到权重向量。
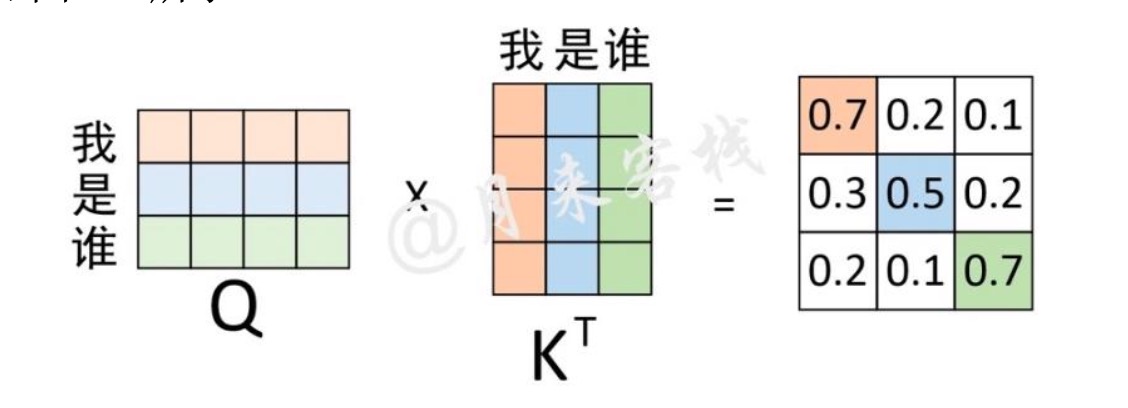 通过这个权重矩阵($QK^T$)模型就能轻松的知道在编码对应位置上的向量时,应该以何种方式将注意力集中到不同的位置上。不过模型在对当前位置的信息进行编码时,会过度的将注意力集中于自身的位置(虽然这符合常识,向量自己与自己的内积最大)而可能忽略了其它位置。因此,作者采取的一种解决方案就是采用多头注意力机制。
通过这个权重矩阵($QK^T$)模型就能轻松的知道在编码对应位置上的向量时,应该以何种方式将注意力集中到不同的位置上。不过模型在对当前位置的信息进行编码时,会过度的将注意力集中于自身的位置(虽然这符合常识,向量自己与自己的内积最大)而可能忽略了其它位置。因此,作者采取的一种解决方案就是采用多头注意力机制。
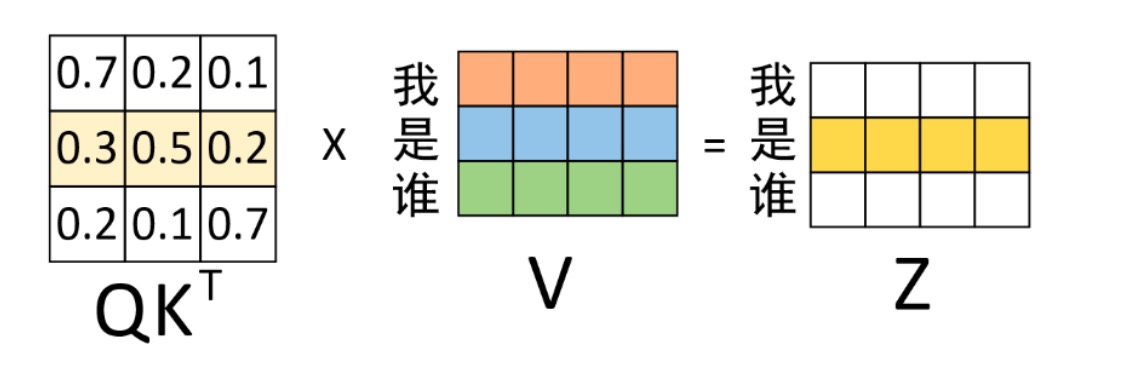
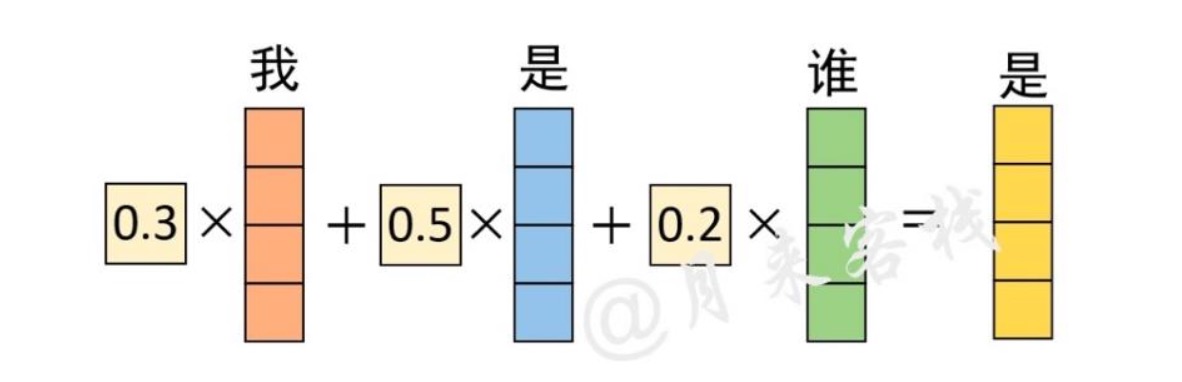
得到权重矩阵后,便可以将其作用于V($QK^T * V = Z$,进而得到最终的编码输出。对于最终输出“是”的编码向量来说,它其实就是原始“我 是 谁”3 个向量加权和,而这也就体现了在对“是”进行编码时注意力权重分配的全过程。
不会 CUDA 也能轻松看懂的 FlashAttention 教程(算法原理篇)Attention 运算建模了一个常见的场景:已有数据a,该如何从数据集合 $B = {b_i}$中提取信息。比如一个像素要从图像中所有像素中提取信息,或者一个句子里的 token (词元)从另一个句子的所有 token 中提取信息。PS:输出这个token揉和其它token后的表示。
PS: 假设我们的目的是为了得到一个对“我”“是”“谁”的最佳emb 向量表示,且特定字符的向量表示不是静态的,且有了已经训练好的$W_q$,$W_k$,$W_v$,那很自然的,就是拿当前字符与所有上下文字符的相似度和来表示这个字符相对这句话的向量表示。感觉dl 就是特征向量化后mlp。
从认知视角来看Attention
当我们谈论 AI 推理的 KV Cache,我们在说什么?在学习了各种资料之后,我逐渐形成了如下认知,私以为这些认知有助于朴实地理解什么是 Attention。
- 我们首先来回答一个问题:你觉得这个世界是可以描述的吗?嗯,我不要你觉得可以,我要我觉得可以。如果这个世界是可以描述的,依赖的自然是一些可观测的特征,譬如词汇(可基于此实现拼写纠错、词表映射、子词合并),语法(可基于此实现解析、信息抽取、依存关系判断),语义(可基于此实现语义检索、同义替换、聚类),实体/属性(人名,地名,机构等实体以及属性,可基于此实现知识抽取,知识问答),事件/时序/因果(可基于此实现摘要、时间线生成、推理),情感/语气/意图(可基于此实现情感分析、对话管理、意图识别),主题/话题分布(可基于此实现分类、检索、路由),……
- 没错,人类认知大千世界大体就是这个思路:“提取”各类事物的特征,然后去做特征“匹配”。不过,LLM 大模型并没有选择基于静态的、离散的特征表条目来演进自身的认知能力,因为这种形式的表述能力太弱;死板的 0/1 匹配亦无法提供近似表示;再者,不具备可微性亦导致无法自动发现有用特征;…… 总之,LLM 大模型选择引入向量这种表示形式。回头想一想,向量这种表示真是很有魔性,好,真好,咋那么好呢!相较于静态、离散的特征表条目,向量表示提供了高效、可微、具泛化能力且能压缩复杂语义的表述方式,甚至很适合用梯度学习从大量文本中自动提取模式,优势不可谓不显著。以 GPT‑3 175B 为例,它内部处理使用的向量维度大小(通常也被称为 hidden size)达到了惊人的 12288!啧啧啧,这表述能力得多强。总之,一个高维的向量表示提供了更多自由度去编码大量交织的属性,譬如词性、实体、时态、事实证据、上下文线索等等。尤其地,向量表示的一个非常厉害的地方在于其提供了平滑泛化的能力,向量空间允许“相似”输入得到“相似”表示,模型可以对未见过的组合或近似表达进行合理推断。譬如你训练过 “red apple” 和 “green pear”,那么在语义空间上就能够推断 “green apple” 背后向量表示的位置。故而,基于一个向量的匹配查询(譬如基于向量内积运算),那么得到的就不是非 0 即 1 的死板的、确定性的查询结果,而是一系列的相似度值。关键点来了,因为向量的近似表示,针对某个查询(以向量的形式),我们会拿到一系列近似表示(同样也是一系列向量)的候选人,我们该如何选择呢?记住了,成年人不做选择!LLM 大模型引入权重矩阵,(也就是所谓的注意力矩阵),用来表示“用多大的权重去关注一众潜在候选人”,主打一个雨露均沾。
